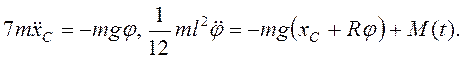
Подставляя в них ![]() , находим
, находим 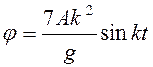 , и
, и
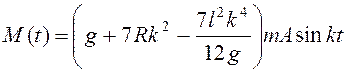 .
.
Ответ: 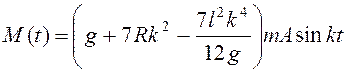 .
.
 43. Для
рассматриваемой системы с двумя степенями свободы в качестве обобщенных
координат возьмем
43. Для
рассматриваемой системы с двумя степенями свободы в качестве обобщенных
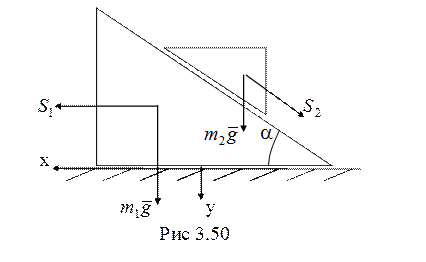
координат возьмем ![]() – смещение 1-й призмы, и
– смещение 1-й призмы, и ![]() – смещение 2-й призмы относительно первой
(рис. 3.50). Тогда кинетическая энергия поступательно движущихся призм
– смещение 2-й призмы относительно первой
(рис. 3.50). Тогда кинетическая энергия поступательно движущихся призм
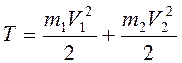 .
.
Составляющая скорости ![]() . По теореме сложения скоростей
. По теореме сложения скоростей ![]() . Принимая за переносное движение движение
первой призмы найдем
. Принимая за переносное движение движение
первой призмы найдем
![]() .
.
Поэтому ![]() .
.
Виртуальная работа сил ![]() , поэтому обобщенные силы
, поэтому обобщенные силы ![]() ,
, ![]() . Составляя
уравнения Лагранжа второго рода
. Составляя
уравнения Лагранжа второго рода 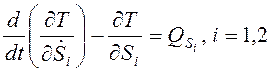 , получим систему
уравнений
, получим систему
уравнений
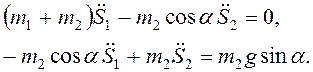
Решая ее относительно ![]() найдем
найдем 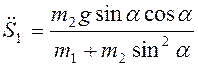 ,
, 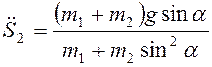 .
.
По теореме сложения
ускорений ![]() . При поступательности переносного движения
ускорение Кориолиса
. При поступательности переносного движения
ускорение Кориолиса ![]() , и
, и
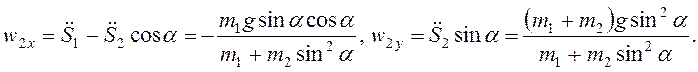
Ответ: 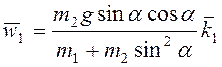 ,
,
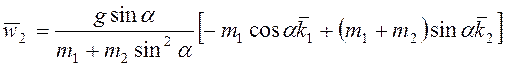 .
.
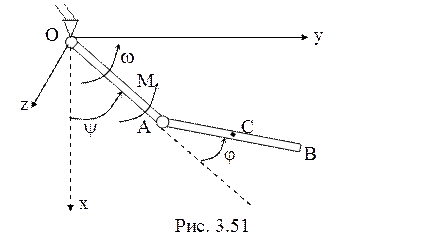 44. В качестве
обобщенных координат рассматриваемой системы с двумя степенями свободы возьмем
углы
44. В качестве
обобщенных координат рассматриваемой системы с двумя степенями свободы возьмем
углы ![]() ,
, ![]() (рис.
3.51). Связи идеальны и голономны, составляем уравнения Лагранжа второго рода
(рис.
3.51). Связи идеальны и голономны, составляем уравнения Лагранжа второго рода
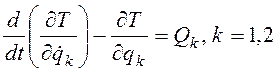 .
.
Кинетическая энергия
системы ![]() . Для стержня ОА
. Для стержня ОА ![]() .
Для стержня АВ
.
Для стержня АВ ![]() . Скорость
. Скорость ![]() , т.е.
, т.е.
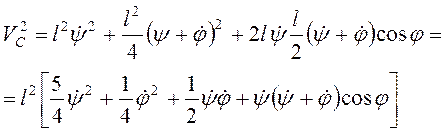 ,
,
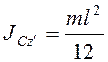 ,
,
![]() , и
, и 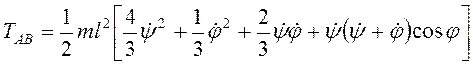 .
.
Для всей системы 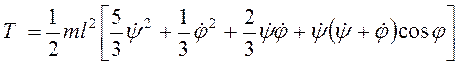 .
.
Обобщенные силы ![]() . Для вычисления левых частей уравнений
Лагранжа выполняем соответствующие операции.
. Для вычисления левых частей уравнений
Лагранжа выполняем соответствующие операции.
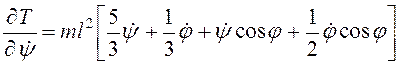
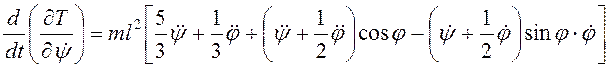 ,
,
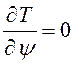
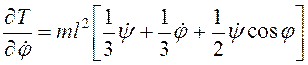 ,
,
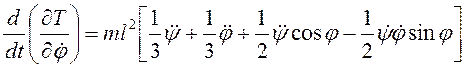 ,
, 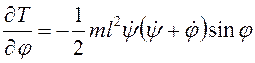
Уравнения Лагранжа второго рода имеют вид
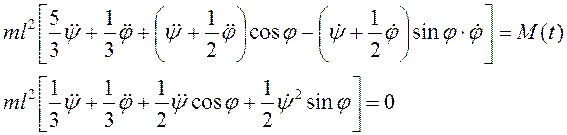
Не ограничивая общности
можем считать ![]() . Тогда
. Тогда
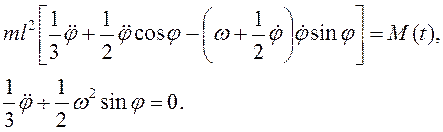
Линеаризация последних уравнений при
малом угле ![]() даст
даст
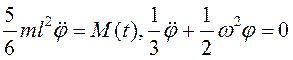 .
.
Подстановкой ![]() получим
получим 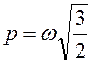 ,
, 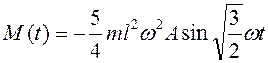 .
.
Ответ: 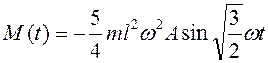 .
.
45. Для рассматриваемой
системы с двумя степенями свободы и голономными идеальными связями (силы реакции
не совершают работу) в качестве обобщенных координат возьмем ![]() (рис. 3.52). Составляем уравнения Лагранжа второго рода
(рис. 3.52). Составляем уравнения Лагранжа второго рода
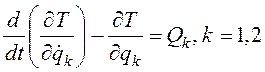 .
.
Кинетическая энергия ![]() . Для трубки
. Для трубки
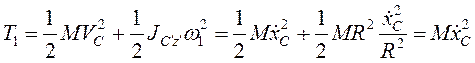 .
.
Для точки ![]() . Составляющие скорости
. Составляющие скорости
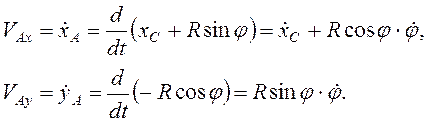
![]() ,
, 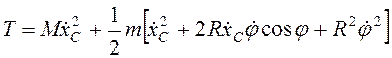 .
.
Работу совершает
консервативная стационарная сила тяжести точки, потенциальная энергия
соответственно ![]() ; обобщенные силы
; обобщенные силы 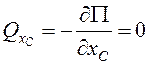 ,
, 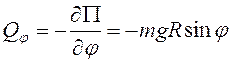 .
.
Дифференцированием вычисляем левые части уравнений Лагранжа.
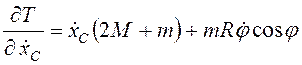
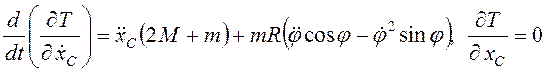
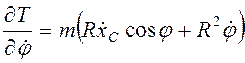 ,
,
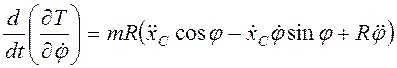
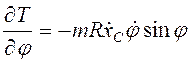
Уравнения Лагранжа принимают вид
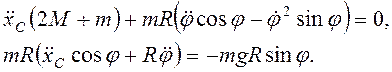 (3.67)
(3.67)
В положении равновесия
системы 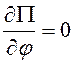 , т.е.
, т.е. ![]() . При
. При ![]() это равновесие неустойчиво, поэтому
возможность малых колебаний рассматриваем около положения равновесия
это равновесие неустойчиво, поэтому
возможность малых колебаний рассматриваем около положения равновесия ![]() . В окрестности этого равновесия линеаризация
уравнений (3.67) даст
. В окрестности этого равновесия линеаризация
уравнений (3.67) даст
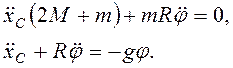
Тогда 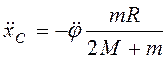 ,
, 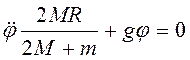 . Общее решение последней системы уравнений
. Общее решение последней системы уравнений
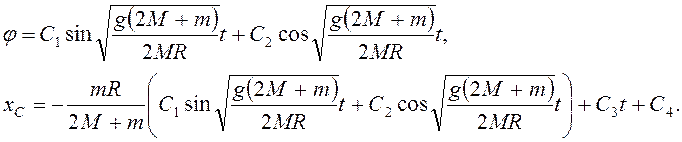 (3.68)
(3.68)
Выражение для угла ![]() при малых отклонениях начальных условий от
равновесия соответствует малым колебаниям, выражение же для
при малых отклонениях начальных условий от
равновесия соответствует малым колебаниям, выражение же для ![]() будет им соответствовать при
будет им соответствовать при ![]() .
.
При заданных начальных
условиях ![]() из (3.68) следует
из (3.68) следует
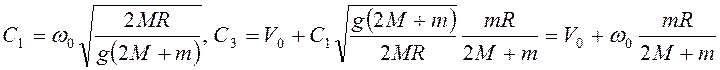 .
Условие
.
Условие ![]() дает
дает 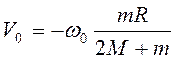 .
.
Ответ: 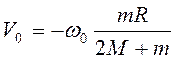 .
.
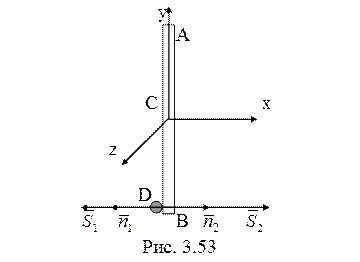 46. Ударные импульсы,
с которыми стержень и точка действуют друг на друга, направлены вдоль оси
46. Ударные импульсы,
с которыми стержень и точка действуют друг на друга, направлены вдоль оси ![]() (рис. 3.53), поэтому по теореме об
изменении импульса для каждого из тел после удара их центры масс также
приобретут скорости, направленные вдоль оси
(рис. 3.53), поэтому по теореме об
изменении импульса для каждого из тел после удара их центры масс также
приобретут скорости, направленные вдоль оси ![]() .
.
По теореме об изменении
импульса для всей системы при ударе ![]() . До удара
. До удара ![]() (
(![]() –
скорость точки до удара), после удара
–
скорость точки до удара), после удара ![]() , и
, и ![]() , т.е.
, т.е.
![]() . (3.69)
. (3.69)
По теореме об изменении
кинетического момента системы относительно оси ![]()
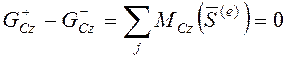 . До удара
. До удара ![]() (
(![]() - длина стержня). После удара
- длина стержня). После удара
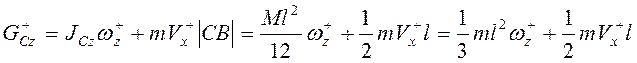 .
.
Тогда ![]() , т.е.
, т.е.
![]() . (3.70)
. (3.70)
Уравнений (3.69) и (3.70)
недостаточно для нахождения кинематических характеристик системы после удара.
Поэтому воспользуемся обобщением гипотезы Ньютона ![]() (
(![]() - коэффициент восстановления). До удара
- коэффициент восстановления). До удара ![]() , после удара
, после удара ![]() (
(![]() - единичные векторы нормали к поверхностям
тел в точке соударения). Тогда
- единичные векторы нормали к поверхностям
тел в точке соударения). Тогда
![]() . (3.71)
. (3.71)
Совместным решением уравнений (3.69)-(3.71) получим
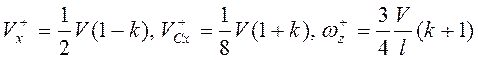 .
.
Последние формулы
используем при постановке начальных условий при рассматрении движения тел по
окончании удара. Для точки ![]() , т.е.
, т.е. ![]() . Для плоскопараллельно движущегося стержня
. Для плоскопараллельно движущегося стержня
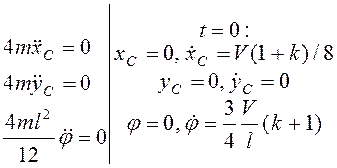 ,
,
т.е. 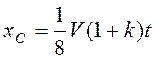 ,
, ![]() ,
, 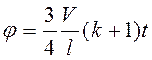 .
.
В момент повторного удара
конца стержня А по точке ![]() . Так как
. Так как 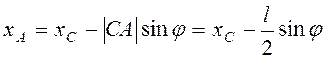 , а удар может произойти при
, а удар может произойти при ![]() , то это соответствует условию
, то это соответствует условию ![]() , т.е.
, т.е. ![]() .
.
Ответ: ![]() .
.
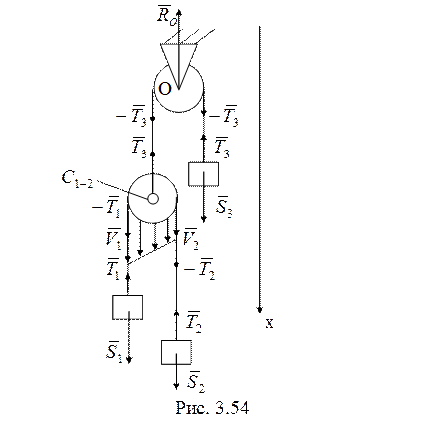
47. Из условия равенства
нулю суммы моментов сил, приложенных к системе, относительно точки О до начала
действия электромагнита (рис. 3.54) следует, что ![]() , т.е.
, т.е. ![]() .
.
 После включения по
теореме об изменении импульса груза 3
После включения по
теореме об изменении импульса груза 3
![]() (3.72)
(3.72)
(![]() -
импульсы натяжения нитей). Эта же теорема для грузов 1-2 вместе с подвижным
блоком даст
-
импульсы натяжения нитей). Эта же теорема для грузов 1-2 вместе с подвижным
блоком даст
![]() .
(3.73)
.
(3.73)
Теорема об изменении кинетического
момента для этой же части системы относительно оси ![]() ,
перпендикулярной плоскости рисунка, даст
,
перпендикулярной плоскости рисунка, даст
![]() . (3.74)
. (3.74)
Учитывая нерастяжимость нити и особенности распределения скоростей при плоскопараллельном движении, имеем уравнение связи
![]() . (3.75)
. (3.75)
Совместным решением уравнений (3.72)-(3.75) найдем
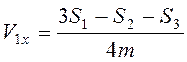 ,
,
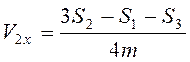 ,
, 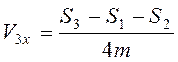 .
.
Ответ: 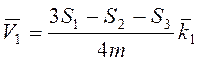 ,
, 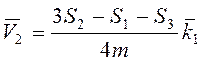 ,
, 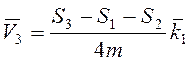 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.