С возрастанием частоты от ω=0 до ω=∞ характеристический
вектор ![]() будет изменять свой аргумент (угол
поворота относительно действительной оси
будет изменять свой аргумент (угол
поворота относительно действительной оси![]() ) в
соответствии со знаком корня характеристического уравнения. Конец этого вектора
будет описывать кривую, которая называется годографом Михайлова. Если в системе
n-го порядка все n корней характеристического уравнения находятся слева от
мнимой оси на комплексной плоскости, то характеристический вектор повернется на
угол
) в
соответствии со знаком корня характеристического уравнения. Конец этого вектора
будет описывать кривую, которая называется годографом Михайлова. Если в системе
n-го порядка все n корней характеристического уравнения находятся слева от
мнимой оси на комплексной плоскости, то характеристический вектор повернется на
угол ![]() с возрастанием частоты от ω=0 до ω=∞.
Следовательно, для устойчивости системы достаточно, чтобы при возрастании
частоты от ω=0 до ω=∞ годограф Михайлова последовательно проходил n квадрантов
на комплексной плоскости.
с возрастанием частоты от ω=0 до ω=∞.
Следовательно, для устойчивости системы достаточно, чтобы при возрастании
частоты от ω=0 до ω=∞ годограф Михайлова последовательно проходил n квадрантов
на комплексной плоскости.
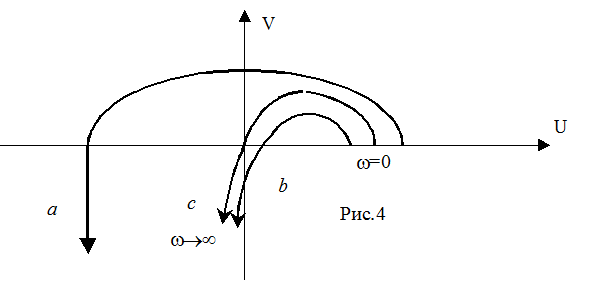
На рис.4 кривая Михайлова (a) соответствует устойчивой системе, кривая (b) – неустойчивой, система с годографом Михайлова (c) находится на колебательной границе устойчивости.
Критерий Найквиста. Часто необходимо определить устойчивость замкнутой системы управления с передаточной функцией Ф(р), если известна передаточная функция разомкнутой системы W(p)
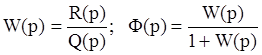 ,
,
здесь порядок полинома R(p) меньше, чем порядок полинома Q(p). (Передаточную функцию W(р) можно получить экспериментально).
Введем вспомогательную функцию
 ,
,
в числителе которой получим характеристический многочлен системы D(p).
Для устойчивой системы в диапазоне частот ![]() годограф
годограф ![]() не
будет охватывать точку (0; j0). Следовательно, обычная комплексная частотная
характеристика разомкнутой системы W(jω) не будет охватывать точку (-1; j0) на
комплексной плоскости.
не
будет охватывать точку (0; j0). Следовательно, обычная комплексная частотная
характеристика разомкнутой системы W(jω) не будет охватывать точку (-1; j0) на
комплексной плоскости.
Поскольку две ветви частотной характеристики W(jω) (для ![]() и для
и для ![]() )
симметричны относительно действительной оси, то для анализа устойчивости
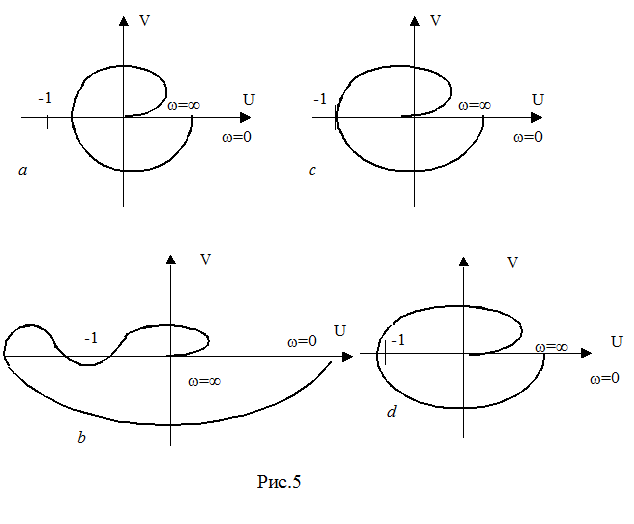
достаточно построить только первую ветвь. На рис. 5 a,b
представлены характеристики W(jω) (годографы Найквиста) для устойчивой системы;
на рис.5 c – кривая W(jω) для системы, находящейся на колебательной
границе устойчивости; на рис. 5 d – для неустойчивой системы.
)
симметричны относительно действительной оси, то для анализа устойчивости
достаточно построить только первую ветвь. На рис. 5 a,b
представлены характеристики W(jω) (годографы Найквиста) для устойчивой системы;
на рис.5 c – кривая W(jω) для системы, находящейся на колебательной
границе устойчивости; на рис. 5 d – для неустойчивой системы.
Система, характеристика которой W(jω) представлена на рис.5 a будет называться абсолютно устойчивой. Это значит, что при любом увеличении коэффициента усиления разомкнутой системы K замкнутая система останется устойчивой.
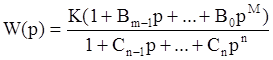
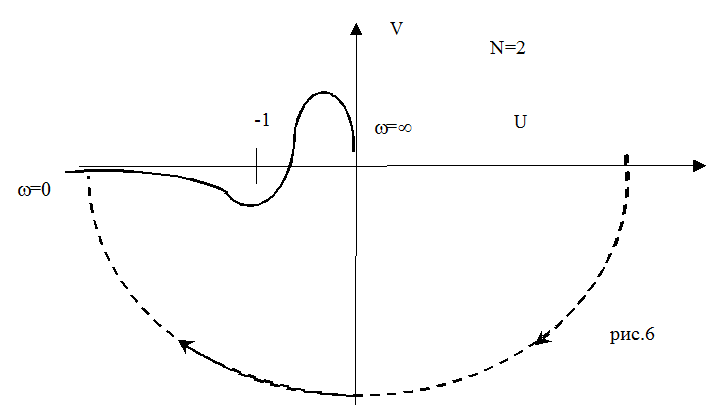
Если передаточная функция W(p) имеет астатизм порядка N, то
при построении годографа Найквиста мы должны дополнить кривую ![]() дугами бесконечного радиуса с изменением
аргумента на (
дугами бесконечного радиуса с изменением
аргумента на (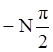 ) , чтобы начало годографа (для
) , чтобы начало годографа (для ![]() ) располагалось на положительной части
действительной оси. (рис.6)
) располагалось на положительной части
действительной оси. (рис.6)
Иногда замкнутая система будет устойчивой даже если передаточная функция разомкнутой системы W(p) имеет корни знаменателя в правой части комплексной плоскости. Для этого случая критерий Найквиста имеет специальную форму. В графической форме это выражается в том, что годограф Найквиста должен охватывать точку (-1; j0) столько раз, сколько знаменатель W(p) имеет корней с положительной действительной частью.
Анализ устойчивости с помощью ЛАФЧХ. Требование
критерия Найквиста, чтобы комплексная частотная характеристика разомкнутой
системы не охватывала точку (-1; j0) на практике означает, что для частоты,
где argW(jω) =(![]() ), должно выполняться условие
|W(jω) |<=1. В противном случае при замыкании системы можно получить условие
самовозбуждения колебаний системы, когда сигнал отрицательной обратной связи
превращается в положительную обратную связь, которая не уменьшает, а
увеличивает рассогласование системы.
), должно выполняться условие
|W(jω) |<=1. В противном случае при замыкании системы можно получить условие
самовозбуждения колебаний системы, когда сигнал отрицательной обратной связи
превращается в положительную обратную связь, которая не уменьшает, а
увеличивает рассогласование системы.
Таким образом можно сказать, что для устойчивости системы
необходимо, чтобы на частоте среза ωс (где A(ωс)=1)
выполнялось условие φ(ωс)>-p.
И наоборот, для частоты ωπ ( где φ(ωπ)=-π ) должно
выполняться условие A(![]() )<=1.
)<=1.
Если перевести эти условия в изображение логарифмической
частотной характеристики, то получим, что при возрастании частоты ЛАЧХ L(![]() ) должна пересекать отметку 0 dB до того,
как ЛФЧХ φ(ω) пересечет отметку (-
) должна пересекать отметку 0 dB до того,
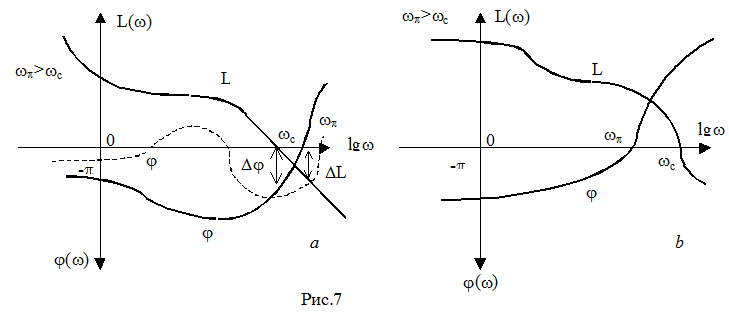
как ЛФЧХ φ(ω) пересечет отметку (-![]() ) rad. На рис.7 a
построены логарифмические АЧХ и ФЧХ для устойчивой системы, на рис.7 b –
для неустойчивой. На рис.7 a представлена также ФЧХ устойчивой системы,
которая соответствует случаю, относящемуся по критерию Найквиста к рис.5 b.
Здесь за частоту ωπ следует принять последнюю точку пересечения
линии φ(ω)=-π фазовой характеристикой при возрастании частоты.
) rad. На рис.7 a
построены логарифмические АЧХ и ФЧХ для устойчивой системы, на рис.7 b –
для неустойчивой. На рис.7 a представлена также ФЧХ устойчивой системы,
которая соответствует случаю, относящемуся по критерию Найквиста к рис.5 b.
Здесь за частоту ωπ следует принять последнюю точку пересечения
линии φ(ω)=-π фазовой характеристикой при возрастании частоты.
Из рис.7 b легко заключить, что для того, чтобы системы стала устойчивой необходимо уменьшить общий коэффициент усиления разомкнутой системы («опустив» кривую L(ω)).
Для устойчивой системы (рис.7 a) можно определить запасы устойчивости по фазе Δφ и по амплитуде ΔL. Обычно для хорошей устойчивости автоматической системы предъявляются требования
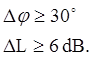
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.