Lecture 10
LOGARITHMIC FREQUENCY CHARACTERISTICS OF ELEMENTARY LINKS
Lecture plan:
1. Logarithmic frequency characteristics of position links
2. Logarithmic frequency characteristics of integrating links
3. Logarithmic frequency characteristics of differentiating links
4. Construction of system’s logarithmic frequency characteristic
As we said before, in certain cases for amplitude and phase frequency characteristics more comfortable is logarithmic scale.
In logarithmic coordinates frequency axis
marked proportional to lg w. This axis divided
in decades: each decade accords to frequency rising in 10 times, for example,
if decade beginning accords to value 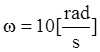 then this decade ends
by value
then this decade ends
by value 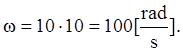
Logarithmic scale for amplitude marked in decibels: One bell accords to power multiplication in 10 times, two Bells – in 100 timed, etc. Formula for translation of linear amplitude characteristics in logarithmic scale:
L(w)=20lg|W(i w)|=20lgA(w). [dB].
Decibel is tenth part of Bell.
Coefficient
20 derives from A(w) isn't a power
ratio, but amplitude ratio. Increase of amplitude in 10 times accords to power
increase in 100 times. Hence, one decibel accords to amplitude increase in ![]() times.
times.
Negative values of L(w) accords to amplitude decrease. For phase frequency characteristics linear scale used.
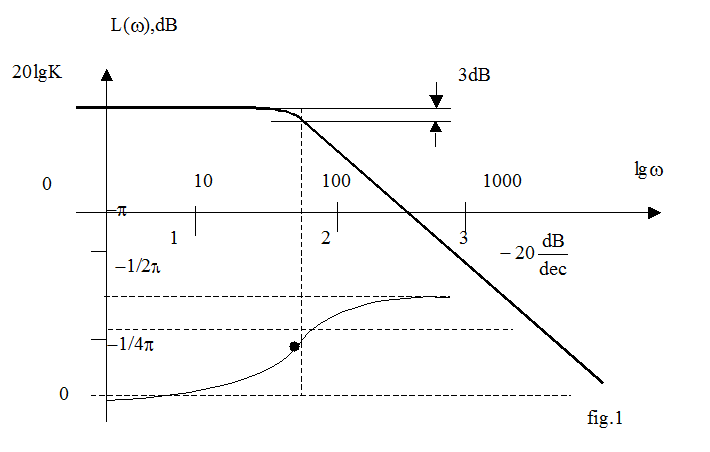
The most important feature of logarithmic frequency characteristic, that in logarithmic coordinates amplitude functions represents by asymptotic straight lines even they represents by curves in linear scale. For phase characteristics: each curve in logarithmic scale keep their shape for all variety of certain type links. This curve shifted along frequency axis only.
Now we show logarithmic frequency characteristics for main elementary dynamic link set.
1. Non-inertia link : W(p)=K
L(w)=20lgK=const
j(w)=0=const.
2. Aperiodic
link: 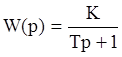
![]()
Ll(w)![]() 20lgK – straight line
parallel to frequency axis.
20lgK – straight line
parallel to frequency axis.
Lh(w)![]() 20lgK-20lgK-20lgw - straight line with constant slope.
20lgK-20lgK-20lgw - straight line with constant slope.
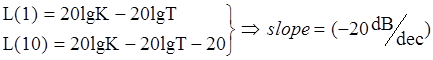
To find frequency of break combine both of cases:
Ll(w)=Lh(w)
20lgK=20lgK-20lgT-20lgw0 Þ
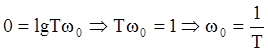
Logarithmic frequency characteristic of aperiodic link represented in fig.1.
For phase frequency characteristics as in linear scale:
![]()
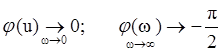
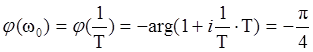
3. Oscillation
link: 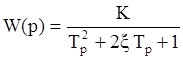
Analog to previous:
![]()
![]()
![]()
Asymptote slope: -40 dB/dec.
Break frequency:
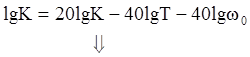
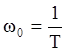 - it is resonance
frequency.
- it is resonance
frequency.
For phase frequency characteristic:
![]()
![]()

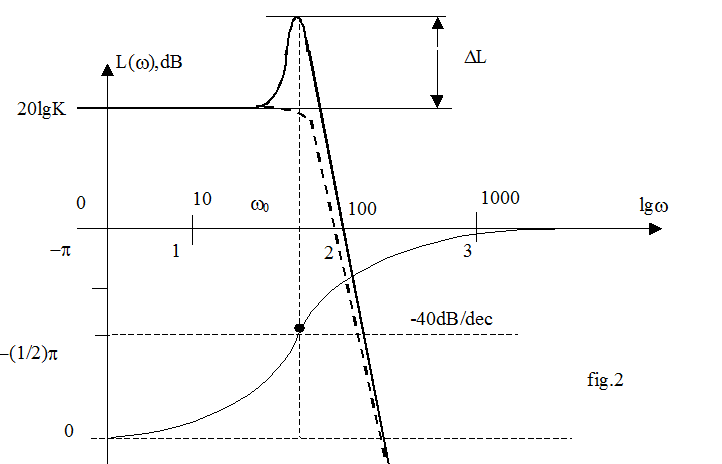
Value of peak DL according to frequency w0 depends on damping coefficient x. The more x the less value of DL. For x®0 (conservative link) we have infinity big value of peak of amplitude characteristic resonance frequency.
4. Integrating
link 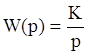
It’s easy to find, that
![]()
For w=1: L(w)=20lgK;
For any value of frequency; logarithmic amplitude frequency characteristic of this link can be exactly represented through straight line with slope –20 dB/dec:
L(10)=20lgK-20lg10=20lgK-20.
As we find for linear scale:
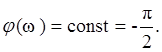
5. Differentiating link W(p)=Kp.
For this
link L(w) is straight line slope +20 dB/dec. And
for w=1 L(w)=20lgK. 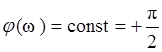 .
.
6. Differentiating link with slowing
W(p)=K(Tp+1)
Logarithmic amplitude for low frequency: ![]() for high frequency:
for high frequency:
![]()
![]()
Hence for
frequency  this characteristic represents through
straight line with slope +20 dB/dec.
this characteristic represents through
straight line with slope +20 dB/dec.
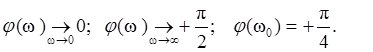
On studied facts base we can derive next rule for logarithmic frequency amplitude-phase characteristics building.
It transfer function of system can be represented through fraction:
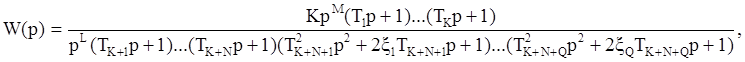
then we can build general logarithmic characteristic as geometry sum of elementary links characteristics.
For w=1 L(w)=20lgK.
Slope of
low-frequency amplitude characteristic equal to 20(M-L) dB/dec. Value (M-L)=N
we shall call as astatism order. This number shows how many zero roots has
denominator of open-loop system’s transfer function. Frequency axis divided by
break frequencies in some segments. In each segment slope of amplitude characteristic
will accord to combination of break frequencies: each value of 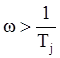 , where Tj-time constant of
aperiodic link - slope is (-20 dB/dec); for
, where Tj-time constant of
aperiodic link - slope is (-20 dB/dec); for 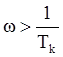 , where
Tk – time constant of oscillation link – slope is (-40 dB/dec).
, where
Tk – time constant of oscillation link – slope is (-40 dB/dec).
Phase frequency characteristic received as geometry sum of according phase characteristics of elementary links too.
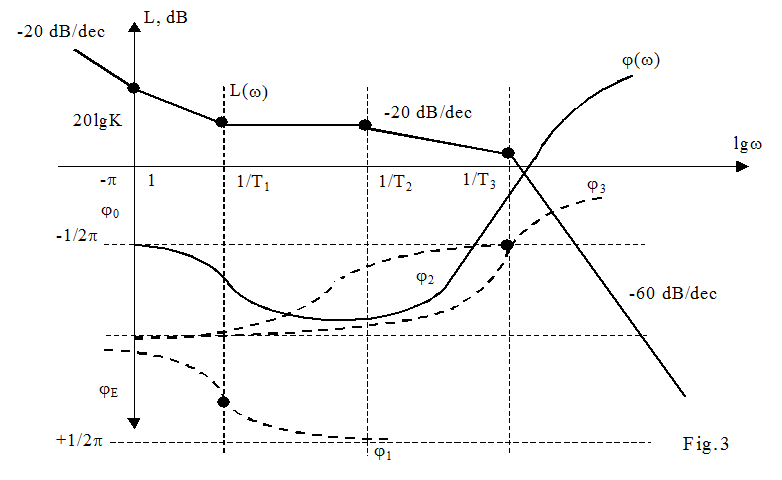
Example:
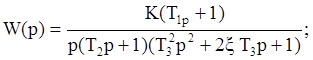
logarithmic frequency characteristic represented in fig.3
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.