Решение задач оптимизации средствами MathCad и Excel (Практическое занятие № 3), страница 3

Использование Mathcad для решения графическим методом

Для рассмотрения возможностей Mathcad для геометрической интерпретации решения задачи оптимизации рассмотрим пример.

Постановка задачи: Промышленное предприятие выпускает продукцию из имеющихся ресурсов. Требуется спланировать выпуск продукции на определенный период так, чтобы обеспечить получение максимальной прибыли. Пусть на предприятии изготавливается 2 вида изделий – А и В, при этом используются три вида ресурсов C, D и E. Исходные данные по расходу ресурсов приведены в таблице 1.1. Количество ресурсов ограничено и равно соответственно 40, 30 и 50 единиц. Известно также, что прибыль от реализации единицы продукции типа  А дает 3 единицы дохода, а типа В – 2 единицы.

Таблица 1.1

Математическая модель. Введем переменные: x₁ - количество изделий типа A и x₂ – количество изделий типа B.

Ограничения по количеству использования ресурсов:

Ресурс  С:    ;

D:      ;

E:       .

Переменные должны быть неотрицательны , .

Целевая функция определяет общий доход от реализации продукции

Для решения этой задачи в Mathcad необходимо выполнить следующую последовательность действий (рис.1.3):

1.  Записать ограничения в виде равенств: 2×x1+ 2×x2 = 40 и т.д.  При этом можно не использовать в названии переменных индексы, но не следует забывать вводить знак умножения, а для ввода знака равенства использовать “логическое равно”, которое вводится комбинацией клавиш Ctrl + “=”.

2.  Разрешить эти равенства относительно x₂, т.е. получить f(x₂). Для этого в ограничении необходимо выделить переменную x₂ синей полурамкой, используя пробел, и выполнить команду Symbolics – Variable – Solve. В результате ниже равенства появится выражение относительно x₁. Например, для первого равенства появится выражение –x1+20. Далее необходимо выделить полученное выражение полурамкой слева и последовательно справа налево добавить знак “:=”, который вводится комбинацией клавиш Ctrl + “:”, параметр и имя функции, например, f1(x1). Аналогичную процедуру проделать со всеми неравенствами и получить функции f2(x1), f3(x1) и т.д.

3.  Построить уровень целевой функции. Для этого представить ее в виде 3x1+2x2=C, где С – некоторая константа, произвольное число. В нашем случае введено: C:=20. Далее выполнить действия, производимые над ограничениями, п.2 и найти функцию z(x1) .

4.  Указать пределы изменения переменной x1 в виде диапазона значений. Для этого задают ее имя, далее следует знак присваивания (Ctrl + “:”), начальное значение – 0 (т.к. учитывая граничные условия , , т.е. нас интересует только первая координатная четверть), знак диапазона клавиша “:” и конечное значение – 30.

5.  Построить графики полученных функций, включая целевую функцию. Для этого необходимо поместить курсор немного ниже введенной информации и либо с помощью математической панели, либо с помощью клавиш Shift+ “2” вызвать рамку координат. Слева от рамки, на месте черного квадратика ввести в столбик через запятую имена функций в виде f1(x1) и т.д.

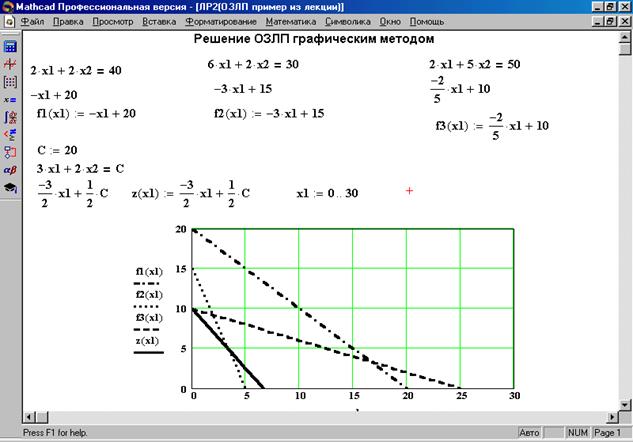
Рисунок 1.3 – Графический метод решения задачи оптимизации

6.  Найти на графике область допустимых решений и определить, если это возможно, на пересечении какие двух прямых находится точка оптимального решения. В нашем случае ОДР – это четырехугольник, находящийся в нижнем левом углу поля графиков, образованный осями координат и прямыми f2() и f3().

7.  Найти точку оптимального решения, т.е. точку пересечения прямых f2() и f3(). Для этого решается система линейных уравнений, в нашем случае это система

.

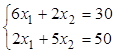              Для того чтобы решить эту систему необходимо ввести (рис. 1.4):

·  начальные приближения для корней, например x1:=0  и x2:=0;

·  служебное слово Given;

·  ввести или скопировать ограничения в виде равенств, записанных используя логическое равно (см. п.1);

·  ввести функцию поиска решения системы с именами неизвестных, Find (x1,x2);

·  нажать клавишу “=”.

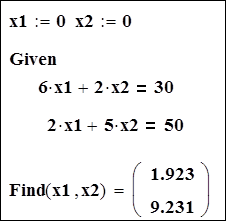
Рисунок 1.4 – Пример решения системы уравнений

Таким образом, получено решение системы x₁=1.923 и x₂=9.231, которое и является оптимальным решением исходной задачи оптимизации. Что означает, что при выпуске продукции вида A в количестве 1.923 условных единиц, а продукции типа B – 9.231, будет получена максимальная прибыль равная  единиц.

Решение задачи оптимизации встроенными средствами MathCad

Смотрите конспект лекций.

Решение задач оптимизации средствами Excel

Смотрите конспект лекций.