Последовательности независимых событий и величин. Неравенство Чебышева. Типы сходимости, страница 4

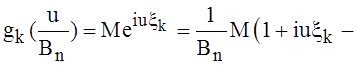
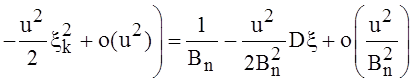.  Значит,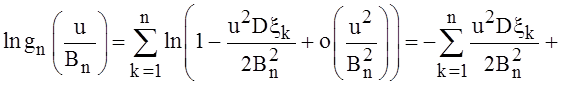

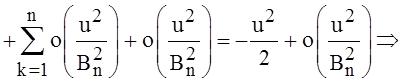
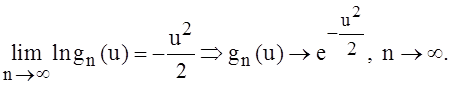
Смысл условия Линдеберга (неравенство 4.7) состоит в следующем. Обозначим за событие

 

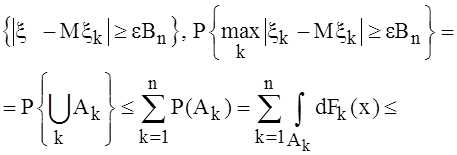
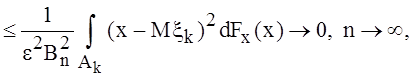
так как событие имеет место при  и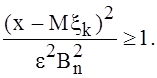  

Таким образом, можно сказать, что смысл условия Линдеберга заключается в равномерной по  малости слагаемых , т.е. среди  нет таких, которые преимущественно определяли бы величину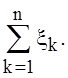

Следствием теоремы 10 является теорема Ляпунова (она появилась раньше, чем теорема Линдеберга).

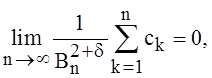Теорема 11 (Ляпунова). Если – последовательность независимых с. величин, для которых существуют и и при некотором  Если существует  где 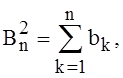 то имеет место равенство (4.6).

Доказательство.

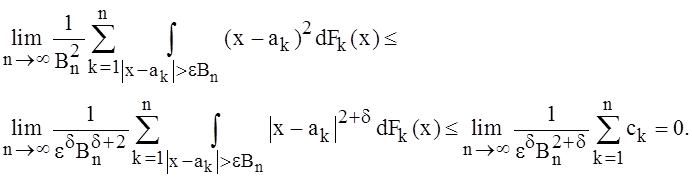
Таким образом, в условиях теоремы неравенство Линдерберга выполняется.

Условие Ляпунова для проверки легче, чем условие Линдерберга.

Следствие.  Если – последовательность независимых одинаково распределенных с. величин с , то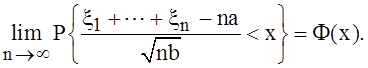

В этом случае

Исключительная важность центральной предельной теоремы объясняется тем, что она дает теоретическое обоснование следующему многократно подтвержденному практикой наблюдению: если исход с. эксперимента определяется большим числом случайных факторов, влияние каждого из которых пренебрежимо мало, то такой эксперимент хорошо аппроксимируется нормальным распределением с соответствующим образом подобранными математическим ожиданием и дисперсией.

Контрольные вопросы

1.  Напишите 1-е и 2-е неравенства Чебышева.

2.  Сформулируйте законы больших чисел.

3.  Дайте определения  всех известных  Вам видов сходимости.

4.  Сформулируйте усиленный закон больших чисел.

5.  Сформулируйте все известные Вам центральные предельные теоремы.

6.   Как вывести интегральную теорему Муавра – Лапласа из центральной предельной теоремы?

Задачи

118. Пусть с.величина h_n равна сумме очков, появившихся при n бросаниях игральной кости. Используя неравенства Чебышева, оценить сверху P{},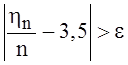

119. Пусть x_k ,k=, - результаты n+1  испытаний схемы Бернулли P{x_k=1)=p,  P{x_k=0)=1-p, и с.величина h_n равна числу таких k, 1£k£n, что  x_k=x_k+1=1. Используя неравенство Чебышева, оценить сверху P{},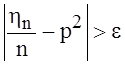

120. С. величины x_k, k=1,2,… независимы и имеют стандартное нормальное распределение, h_n=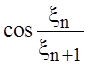, n=1,2,… Удовлетворяют ли последовательности h₁,h₃,h₅,…  и h₁,h₂,h₃,… закону больших чисел?

121. Последовательность x₁,x₂,… с.величин  и с.в. x удовлетворяют условию 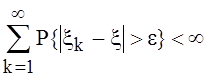,.  Показать, что P{}=1.

122. Последовательность с.в. {x_n} и с.в. x  удовлетворяют условию 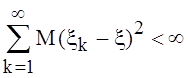. Показать, что P{}=1.

123. С.величины x₁,x₂,…x_n… имеют математическое ожидание и дисперсию σ²<¥. И не коррелированны. Доказать, что P{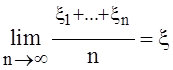}=1.

124. В условиях задачи 118 выбрать n так, чтобы P{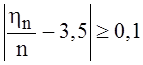}£0,1.

125. С.величины x₀,x₁… независимы и имеют стандартное нормальное распределение. Распределение с.величины 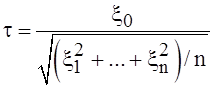   называют распределением Стьюдента с n степенями свободы. Найти

126. C.величина x распределена по закону Пуассона с параметром l. Найти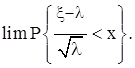

127. С. величина x имеет распределение Коши с параметром  а: 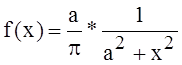, xÎR, показать, что характеристическая функция распределения .

Список использованной литературы

1.  А.А.Боровков.  Курс теории вероятностей.—М.: Наука,1972

2.  М. Лоэв. Теория вероятностей.-М.: Иностранная литература, 1962

3.  Дж. Л. Дуб. Вероятностные процессы.-М.: Иностранная литература, 1956

4.  И.И.Гихман, А.В.Скороход, М.И. Ядренко. Теория вероятностей и математическая статистика.-Киев, «Вища школа», 1979

5.  П. Уиттл. Вероятность.-М.: Наука, 1982

6.  П.П. Бочаров, А.В. Печенкин. Теория вероятностей. Математическая статистика.-М.:Герольдика,1998

7.  А.В. Скороход. Элементы теории вероятностей и случайных процессов.-Киев, ” Вища школа”, 1980

8.  А.И. Зубков, Б.А. Севастьянов, В.П. Чистяков. Сборник задач по теории вероятностей.-М.: Наука,1989