|
|
|
|
|
|
|
|
Примечание: Вопросы для зачета по 1-ой схеме в конце 2-ой лабораторной работы.
Приступим к выполнению пункта №2:
2.ИССЛЕДОВАНИЕ ЦЕПИ R-C СИНУСОИДАЛЬНОГО ТОКА.
A.Теоретические сведения.
Исходная схема имеет вид (рис.2.14). Обсудим расчет этой схемы. В схеме нет узлов, одна ветвь, один контур. Следовательно, можно составить одно уравнение по
|

|
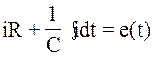 (2.6)
(2.6)
R Решение дифференциального уравнения (2.2), позво -
|
|
На (рис. 2.15) показан характерный для данной цепи график i(t), рассчитанный программой EWB.
Рис.2.14. Исходная схема
|
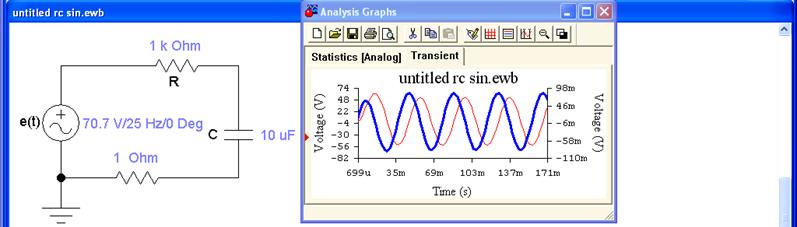
![]() Рис.2.15 График тока в цепи R-C при
включении на синусоидальное напряжение
Рис.2.15 График тока в цепи R-C при
включении на синусоидальное напряжение
Тонкая линия-это график изменения uC(t), жирная линия-это график изменения тока. На этой кривой можно выделить два участка времени: 0 ≤ t ≤ 50мС: на этом участке график изменения тока отличается от синусоидального, в схеме идет переходный процесс и: t ≥0 5мС... К началу второго участка, переходный процесс заканчивается, в схеме наступает принужденный режим. Принужденный режим- это частное решение дифференциального уравнения (2.2), а так как, е(t) меняется по синусоидальному закону, то и ток в этом режиме меняется по синусоидальному закону, а поэтому для расчета используем символический метод.
Э.д.с. е(t)= Emsin(ωt +γ) поставим в соответствие комплекс: Em =Еmejγ , а рассчитываемому току i(t) комплекс Im=Imejα. В уравнении (2.2) присутствует производная тока. Мы не знаем ни амплитуды тока (Im), ни начальной фазы (α), но мы знаем, что ток i(t)= Imsin(ωt+α). Интеграл тока по времени равен:
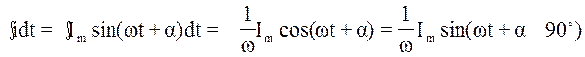
Эта функция отличается от функции тока множителем 1/ω
и начальной фазой -90○, поэтому, ей на комплексной плоскости будет
соответствовать вектор, длина котор- ого в 1/ω раз больше длины вектора тока и
повернут относительно последнего на угол -90○.Учитывая это, можно
записать: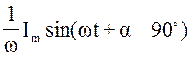 ~
~ 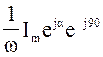 .
.
По
формуле Эйлера: е-j90 =сos(-90○)+jsin(-90○=-j, но
-j=-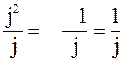 . Таким образом
. Таким образом
![]() ~
~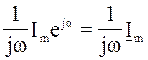 . А
уравнению (2.6) будет соответствовать уравнение
. А
уравнению (2.6) будет соответствовать уравнение
ImR+Im(
![]() ) =Em. Разделив на
) =Em. Разделив на ![]() , получим: IR+I(
, получим: IR+I(![]() ) =E (2.7)
В (2.7):
) =E (2.7)
В (2.7): 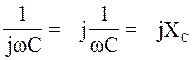 -
комплекс емкостного сопротивления. Очевидно,
сопро
-
комплекс емкостного сопротивления. Очевидно,
сопро
|
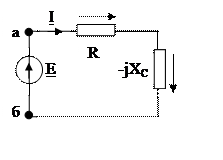 2-му закону Кирхгофа для расчетной схемы
(рис.2.16).
2-му закону Кирхгофа для расчетной схемы
(рис.2.16).
Общее (входное) сопротивление схемы-ZВХ относитель-
|
|
![]() - модуль входного сопротивления
- модуль входного сопротивления
Рис.2.16 Расчетная схема
φ= 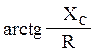 - аргумент входного сопротивления.
- аргумент входного сопротивления.
Используя закон Ома в
символической форме, получим: 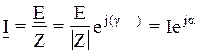 .
.
По известному току I, применяя закон Ома получаем комплексы напряжении на резисторе R: UR = IR и емкости С: UC= I(-jXC ), а затем находим функции (таб.2.10)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.