Проверка гипотез. Представление результатов проверки статистических гипотез в публикациях, страница 2

По таблице стандартного нормального распределения устанавливаем, что значение z, приближенно равное -1,96, отсекает площадь, равную 2,5%, в левом конце распределения, и значение z, приближенно равное 1,96, отсекает площадь, равную 2,5%, справа. Говорят, что z=1,96 (по модулю) является пороговым или критическим значением.

Очень важно понять следующее обстоятельство. Мы не можем построить распределение выборочной статистики для любого значения переменной, например, для того, что было получено в нашем частном исследовании. Дело в том, что у нас нет возможности точно установить истинное положение дел. Воспроизведя свое исследование неоднократно, мы, как правило, будем получать разные значения средних, что является следствием ошибок выборки. Как мы будем формулировать гипотезу: μ=105? μ=106? μ=107,5? Никакой содержательной теории, которая позволила сформулировать конкретную теорию о величине различия, нет. Гипотеза об отсутствии различий (или о нулевом различии) между генеральной совокупностью и выборкой совершенно конкретна и является естественной отправной точкой в статистическом выводе.

Как правило, действительная цель исследования состоит в том, чтобы показать отличия от гипотетической совокупности. Например, в нашем примере мы хотим доказать, что первенцы обладают более высоким интеллектом, чем дети вообще. Статистическая гипотеза, которую мы будем проверять, противоположна исследовательской гипотезе. Это рассуждения от противного. Проверяемая статистическая гипотеза традиционно называется нуль-гипотезой и обозначается H₀. В сущности, статистическая гипотеза – это простое утверждение о параметрах генеральной совокупности.

Словесная формулировка статистической нуль-гипотезы для нашего примера такова: уровень интеллекта первенцев не отличается от уровня интеллекта детей из генеральной совокупности («детей вообще»). Формальная запись выглядит так:

H₀: μ = μ₀ или

H₀: μ = 100.

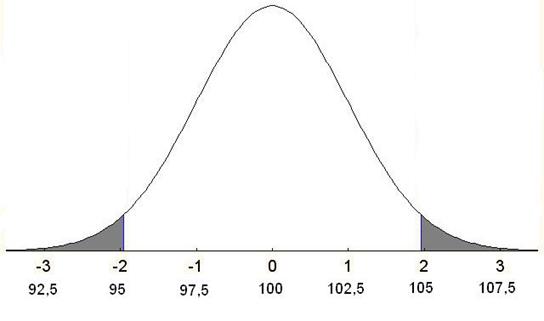
Рис. 1. Распределение выборочных средних для примера с интеллектом первенцев (под осью абсцисс – стандартизованные и «сырые» значения)

Как только мы построили выборочное распределение, дальнейшая процедура проверки этой гипотезы становится очень простой. Мы сравниваем полученное значение среднего с выборочным распределением. Если оно попадает в область отвержения гипотезы (закрашенные области на рис. 1), мы отвергнем нуль-гипотезу. Если оно попадет в незакрашенную область выборочного распределения, у нас не будет оснований для отвержения нуль-гипотезы, но больше определенности достигнуть не удастся: мы по-прежнему не знаем, объясняется ли разность между μ₀ и  тем, что  принадлежит к другой генеральной совокупности, выборочной ошибкой или каким-то иными случайными обстоятельствами.

Чтобы определить, попадает ли  в область отвержения, необходимо его стандартизовать, т.е. преобразовать в z-оценку.

.

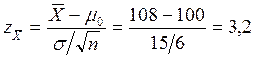Это заведомо больше, чем критическое значение z=1,96. Таким образом, мы отклоняем нуль-гипотезу о том, что интеллект первенцев равен интеллекту детей вообще, или, что то же самое, что выборка первенцев извлечена из генеральной совокупности всех детей. Если нуль-гипотеза верна, вероятность получения результата, меньшего чем –1,96 или большего чем 1,96, составляет 0,05. Поэтому принято говорить, что различия между выборочным средним и средним генеральной совокупности статистически значимы на уровне 0,05, или на уровне 5% (statistically significant at 5% level). Это принято записывать так: p < 0,05.

Вообще говоря, используя таблицу нормального распределения, вы можете убедиться, что вероятность получения =108 при условии, что нуль-гипотеза верна, составляет примерно 0,0014. Другими словами, мы можем сформулировать результат проверки гипотез более точно: различия между средними статистически значимы (p = 0,0014).

Теперь представим процедуру проверки статистических гипотез в виде последовательности шагов.

1. Формулируем исследовательскую гипотезу (обычно она касается наличия различий или связей).