Лабораторная работа №3
Решение систем линейных алгебраических уравнений
Цель работы
Практика использования итерационных методов решения системы линейных алгебраических уравнений. Сравнительный анализ методов.
Постановка задачи
Решить систему линейных алгебраических уравнений (САУ)
![]() ,
, ![]() ,
, ![]() ,
, ![]()
итерационными методами Зейделя и наискорейшего спуска с точностью до e = 0,001. Для сравнения с истинными значениями корней выполнить решение указанной САУ методом Гаусса.
Исходные данные
|
№ |
||||||
|
5 |
A |
0,380 |
- 0,050 |
0,010 |
0,020 |
0,070 |
|
0,052 |
0,595 |
0,000 |
- 0,040 |
0,040 |
||
|
0,030 |
0,000 |
0,478 |
- 0,140 |
0,080 |
||
|
0,060 |
0,126 |
0,000 |
0,470 |
- 0,020 |
||
|
0,250 |
0,000 |
0,090 |
0,010 |
0,560 |
||
|
5 |
b |
1,520 |
- 1,269 |
3,500 |
- 2,988 |
3,390 |
Общий вид алгоритма Зейделя и наискорейшего спуска
Метод Зейделя заключается в том, что найденное на ![]() -ой итерации значение какой-либо
компоненты вектора решения на этой же итерации используется для вычисления
остальных компонент определяемого решения. Именно поэтому метод Зейделя
называют одношаговым алгоритмом, он является представителем группы линейных
алгоритмов первого порядка.
-ой итерации значение какой-либо
компоненты вектора решения на этой же итерации используется для вычисления
остальных компонент определяемого решения. Именно поэтому метод Зейделя
называют одношаговым алгоритмом, он является представителем группы линейных
алгоритмов первого порядка.
Расчетные соотношения метода Зейделя для подготовленной системы уравнений (4.13) имеют вид
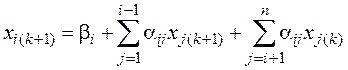 ,(4.18)
,(4.18)
![]() .
.
При составлении программы для вычислений на ЭВМ вместо соотношения (4.18) удобнее использовать выражение, в котором фигурируют элементы исходной системы уравнений
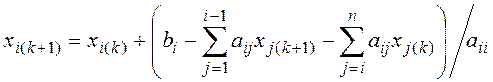 ,
,
![]() .
.
Если матрица ![]() симметрическая
и положительно определенная, а подготовленная к итерациям система определяется
в виде
симметрическая
и положительно определенная, а подготовленная к итерациям система определяется
в виде
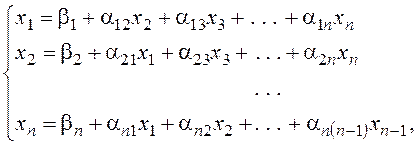 (4.13)
(4.13)
где 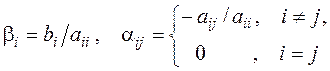 то метод Зейделя
сходится. Если же диагональные элементы симметрической матрицы
то метод Зейделя
сходится. Если же диагональные элементы симметрической матрицы ![]() не отрицательны, то условие
положительной определенности матрицы
не отрицательны, то условие
положительной определенности матрицы ![]() является и необходимым.
является и необходимым.
Из неособенной матрицы ![]() можно получить симметрическую положительно
определенную матрицу путем первой трансформации Гауcса, что осуществляется за
счет умножения слева на матрицу транспонированную
можно получить симметрическую положительно
определенную матрицу путем первой трансформации Гауcса, что осуществляется за
счет умножения слева на матрицу транспонированную ![]() левой и правой частей исходной системы
алгебраических уравнений. При этом решаемая система принимает вид
левой и правой частей исходной системы
алгебраических уравнений. При этом решаемая система принимает вид
![]() .
.
Метод наискорейшего спуска. Данный метод относится к группе
нелинейных градиентных алгоритмов. Градиентные алгоритмы, уточнение решения в
которых осуществлялось по отдельным координатам, предполагают траекторию
движения к истинному решению сразу по всем координатам по линии наискорейшего
спуска в направлении, противоположном вектору градиента функционала, связанного
с ошибкой между истинным решением и решением на ![]() -й итерации. Именно такой выбор направления обеспечивает
наиболее быстрое убывание функционала ошибки. Вычислительная схема метода
наискорейшего спуска выглядит следующим образом. Задаются некоторым начальным
приближением
-й итерации. Именно такой выбор направления обеспечивает
наиболее быстрое убывание функционала ошибки. Вычислительная схема метода
наискорейшего спуска выглядит следующим образом. Задаются некоторым начальным
приближением ![]() (если нет
никакой априорной информации, то полагают
(если нет
никакой априорной информации, то полагают ![]() ), а далее осуществляется итерационный процесс
уточнения
), а далее осуществляется итерационный процесс
уточнения
![]() , (4.19)
, (4.19)
где ![]() - вектор
невязки, представляющий собой ошибку в виде разности между правой и левой
частями системы уравнений, компоненты которого определяются как
- вектор
невязки, представляющий собой ошибку в виде разности между правой и левой
частями системы уравнений, компоненты которого определяются как
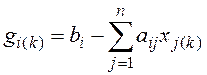 , (4.20)
, (4.20)
а коэффициент
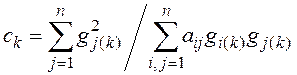 . (4.21)
. (4.21)
Чтобы упростить процедуру определения вектора невязки, особенно при
больших порядках ![]() матрицы
системы уравнений, рекомендуется вычислять его по формуле
матрицы
системы уравнений, рекомендуется вычислять его по формуле
![]() .
.
Однако из-за наличия вычислительных погрешностей векторы ![]() после нескольких итераций
могут отклоняться от истинных невязок и потому время от времени их следует
корректировать по выражению (4.20).
после нескольких итераций
могут отклоняться от истинных невязок и потому время от времени их следует
корректировать по выражению (4.20).
Если матрица ![]() системы
уравнений симметрическая и положительно определенная, то метод наискорейшего
спуска сходится к истинному решению со скоростью геометрической прогрессии.
системы
уравнений симметрическая и положительно определенная, то метод наискорейшего
спуска сходится к истинному решению со скоростью геометрической прогрессии.
Описание программы
Подпрограммы
SUBROUTINE N1YMGS (A,B,N,G,X),
SUBROUTINE N1YMNS (A,B,N,G,X)
реализуют алгоритмы решения САУ методами Зейделя и наискорейшего спуска (одна итерация) соответственно.
Входные параметры подпрограмм:
А(N,N) - (N ´ N)-мерная матрица САУ;
B(N) - N-мерный вектор правой части САУ;
N - мерность САУ;
G(N) - N-мерный вектор невязки (g = b - Ax);
X(N) - N-мерный вектор начальных условий решения САУ.
Выходные параметры подпрограммы:
X(N) - N-мерный вектор уточненных значений решения САУ.
Окончание
итерационной процедуры производиться при выполнении условия ![]() , где
, где 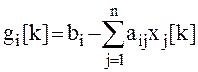 ,
i
,
i![]() [1, n], k = 1, 2, 3, …,
[1, n], k = 1, 2, 3, …,
Подпрограмма
SUBROUTINE N1YGAU (A,B,X,N)
реализует алгоритм метода Гаусса с выбором главного элемента.
Входные A, B, N и выходной X параметры подпрограммы N1YGAU совпадают по описанию с аналогичными параметрами в подпрограммах N1YMGS, N1YMNS.
В подпрограмме N1YGAU матрица A приводится к треугольной.
Результаты вычислений
Таблица1
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.