Министерство образования Российской Федерации
Новосибирский государственный технический университет
Лабораторная работа №3
Вычислительная математика
РЕШЕНИЕ СИСТЕМЫ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ Вариант №6.
Студент:
Земцов Н.
Группа:
АА-86
Проверил:
Чикильдин Г.П.
Новосибирск
2010 г.
1. Цель работы
Практика использования итерационных методов решения системы линейных алгебраических уравнений. Сравнительный анализ методов.
2. Постановка задачи
Решить систему линейных алгебраических уравнений (САУ)
![]() ,
, ![]() ,
, ![]() ,
, ![]()
итерационными методами Зейделя и наискорейшего спуска с точностью до e = 0,001. Для сравнения с истинными значениями корней выполнить решение указанной САУ методом Гаусса.
3. Порядок выполнения работы
1. Ознакомиться с описанием работы. Уяснить цель и смысл задачи согласно варианту (см. табл. 3.1).
2. Записать в общем виде алгоритмы Зейделя и наискорейшего спуска.
3. Решить САУ с выводом результатов на каждой итерации методом
Зейделя с начальными условиями ![]() и
и
![]()
![]() ,
, ![]() .
.
4. Решить САУ с выводом результатов на каждой итерации методом
наискорейшего спуска с начальными условиями ![]() и
и ![]()
![]() ,
, ![]() .
.
5. Решить САУ методом Гаусса.
6. Сравнить результаты, в том числе скорость сходимости итерационных алгоритмов.
7. Оформить отчет.
Примечания:
1) пункты 3, 4, 5 выполняются по алгоритмам, реализованным в подпрограммах N1YTGA, N1YMGS, N1YMNS, N1YGAU, листинги которых приведены в приложении;
2) в подпрограмме N1YGAU матрица A приводится к треугольной, т.е. исходная матрица A портится;
3) при выполнении работы студенты должны составить головную программу, в которой необходимо осуществить:
а) ввод данных,
б) обращение к соответствующим подпрограммам N1YMGS и N1YMNS, в
которых выполняется только одна итерация, а окончание итерационной процедуры производить при выполнении условия
Таблица 3.1
|
6 |
A |
0,490 |
0,000 |
- 0,128 |
0,090 |
0,150 |
|
- 0,030 |
0,320 |
0,000 |
- 0,061 |
0,020 |
||
|
0,010 |
- 0,090 |
0,580 |
0,011 |
0,035 |
||
|
0,030 |
0,000 |
- 0,073 |
0,580 |
0,000 |
||
|
0,020 |
- 0,030 |
0,145 |
- 0,012 |
0,420 |
||
|
6 |
B |
0,964 |
1,279 |
- 1,799 |
- 4,971 |
2,153 |
![]() ,
,
где 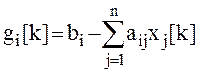 ,
i
,
i![]() [1, n], k = 1, 2, 3, …,
[1, n], k = 1, 2, 3, …,
REAL A(5,5),B(5),G(5),X(5)
DATA X/ 0 , 0 , 0 , 0 , 0 /
DATA A/ 0.490,-0.030, 0.010, 0.030, 0.020,
* 0.000, 0.320,-0.090, 0.000,-0.030,
* -0.128, 0.000, 0.580,-0.073, 0.145,
* 0.090,-0.061, 0.011, 0.580,-0.012,
* 0.150, 0.020, 0.035, 0.000, 0.420/
DATA B/ 0.946, 1.279,-1.799,-4.971, 2.153/
K=0
N=5
E=0.001
2 WRITE (1,101) K,(X(i),i=1,N)
CALL N1YMGS(A,B,N,G,X)
K=K+1
GM=abs(G(1))
DO 1 i=2,N
1 if (abs( G(i) ) > GM) GM=abs(G(i))
if (GM>=E) goto 2
WRITE(1,*)
DO 3 i=1,N
3 X(i)=B(i)/A(i,i)
K=0
5 WRITE (1,101) K,(X(i),i=1,N)
CALL N1YMGS(A,B,N,G,X)
K=K+1
GM=abs(G(1))
DO 4 i=2,N
4 if (abs( G(i) ) > GM) GM=abs(G(i))
if (GM>=E) goto 5
K=1
CALL N1YGAU(A,B,X,N)
WRITE(1,*)
WRITE(1,101) K,(X(i),i=1,N)
101 FORMAT(1x,I1,1x,F8.5,1x,F8.5,1x,F8.5,1x,F8.5,1x,F8.5)
STOP
END
Приведенный листинг выполняет задачу методом Зейделя (N1YMGS), для выполнения задачи методом наискорейшего спуска была написана аналогичная программа с использованием подпрограммы N1YMNS.
5. Результаты вычислений
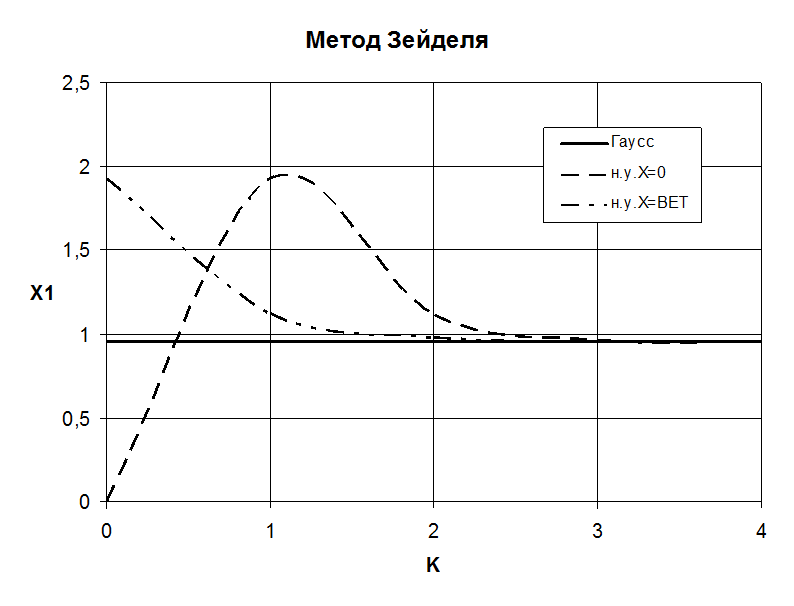
Метод Зейделя:
Нач. условия x(i)=0; i=1,n:
K x(1) x(2) x(3) x(4) x(5)
0 0.00000 0.00000 0.00000 0.00000 0.00000
1 1.93061 4.17787 -2.48672 -8.98353 5.93451
2 1.11437 2.01795 -2.99555 -9.00536 5.99415
3 0.96720 1.99627 -2.99956 -8.99825 6.00119
4 0.96269 1.99676 -2.99996 -8.99807 6.00159
Нач. условия x(i)=BET(i); i=1,n:
0 1.93061 3.99688 -3.10172 -8.57069 5.12619
1 1.12533 2.14820 -2.93458 -8.99825 5.98208
2 0.98552 2.00010 -2.99869 -8.99909 6.00027
3 0.96336 1.99672 -2.99991 -8.99809 6.00153
Метод Гаусса:
1 0.96242 1.99675 -2.99999 -8.99806 6.00161
Сходимость оценки первого корня к истинному значению:
K x(1) x(1) x(1)
Гаусс н.у.Х=0 н.у.Х=ВЕТ
0 0.96242 0.00000 1.93061
1 0.96242 1.93061 1.12533
2 0.96242 1.11437 0.98552
3 0.96242 0.96720 0.96336
4 0.96242 0.96269 0.96336
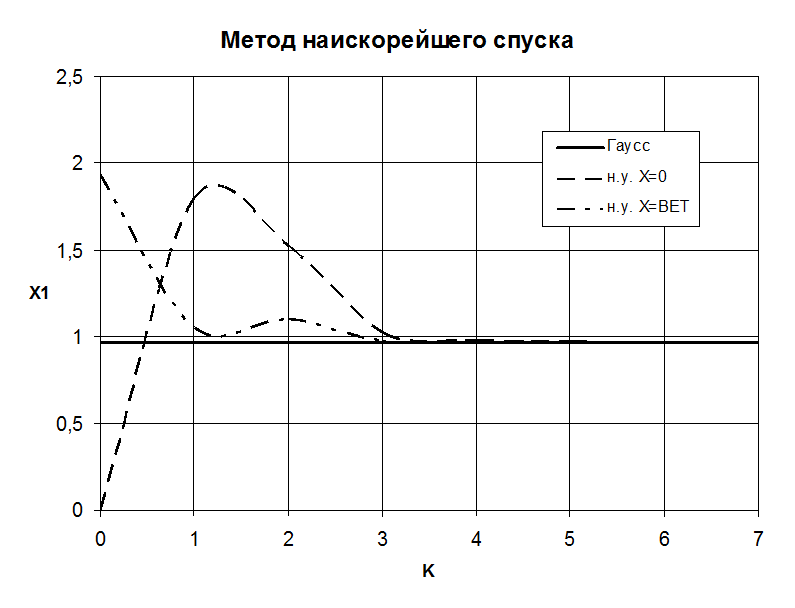
Метод наискорейшего спуска:
Нач. условия x(i)=0; i=1,n:
K x(1) x(2) x(3) x(4) x(5)
0 0.00000 0.00000 0.00000 0.00000 0.00000
1 1.79467 2.42641 -3.41290 -9.43054 4.08448
2 1.51773 2.21882 -2.70757 -9.02651 5.85170
3 1.02609 2.09419 -3.05845 -8.97681 5.88870
4 0.98325 2.04762 -2.97559 -9.01031 5.99337
5 0.97096 2.00558 -2.99982 -8.98891 5.99566
6 0.96339 2.00208 -2.99849 -8.99917 6.00061
7 0.96330 1.99743 -2.99944 -8.99721 6.00150
Нач. условия x(i)=BET(i); i=1,n:
0 1.93061 3.99688 -3.10172 -8.57069 5.12619
1 1.05139 2.73255 -2.53292 -9.20427 6.08030
2 1.09932 2.21672 -2.96334 -8.88878 5.90702
3 0.96965 2.08774 -2.96495 -9.03359 5.99547
4 0.98066 2.02043 -2.99018 -8.98367 5.99472
5 0.96312 2.00715 -2.99826 -9.00172 5.99911
6 0.96443 1.99929 -2.99814 -8.99668 6.00149
Метод Гаусса:
1 0.96242 1.99675 -2.99999 -8.99806 6.00161
Сходимость оценки первого корня к истинному значению:
K x(1) x(1) x(1)
Гаусс н.у.Х=0 н.у.Х=ВЕТ
0 0.96242 0.00000 1.93061
1 0.96242 1.79467 1.05139
2 0.96242 1.51773 1.09932
3 0.96242 1.02609 0.96965
4 0.96242 0.98325 0.98066
5 0.96242 0.97096 0.96312
6 0.96242 0.96339 0.96443
7 0.96242 0.96330 0.96443
Вывод: входе
лабораторной работы я научился использовать итерационные методы решения СЛАУ, а
именно метод Зейделя и метод наискорейшего спуска, можно отметить что при
выборе начальных условий в виде ![]()
![]() ,
, ![]() , оба метода сходятся к истинному
решению за меньшие число итераций, чем при начальных условия в виде
, оба метода сходятся к истинному
решению за меньшие число итераций, чем при начальных условия в виде ![]() ,
, ![]() . При одинаковых условиях окончания
итерационной процедуры метод Зейдера пришел к необходимому результату за
меньшее число итераций.
. При одинаковых условиях окончания
итерационной процедуры метод Зейдера пришел к необходимому результату за
меньшее число итераций.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.