Дифференцируемость функции. Частное приращение, частный дифференциал и частная производная, страница 5

      Однако напомним, что все сказанное относится к случаю, когда аргументы   – независимые переменные, потому что в этом случае   Возможно рассмотрение функции , у которой  , в свою очередь, являются функциями другой переменной (или других переменных). Это сложные функции,  дифференцирование которых в одномерном случае мы уже изучали [1], [2], [5].

4.8. Дифференцирование сложной функции

Рассмотрим теперь функцию y = f(x), которая определена на множестве  X  точек n-мерного пространства:  xÎX,XÌ Rⁿ и множество значений функции это множество Y  точек  m-мерного пространства:  yÎY,   YÌ R^m:

y = f(x), xÎX,   X Ì Rⁿ,     yÎY,   Y Ì R^m.          (4.8.1)

Другая функция, определенная на множествеТ, ТÌ R^l, имеет множество значений  X:

x = g(t),   tÎT,   TÌ R ^l,   xÎ X,   X Ì Rⁿ.             (4.8.2)

Иначе говоря, имеют место отображения множеств:

TХ,     XY, 

которые определяют сложную функцию.

y = f(g(t)),  tÎT,   TÌ R ^l,   yÎY,   Y Ì R^m.          (4.8.3)

      Следующая теорема выясняет достаточные условия дифференцируемости сложной функции.

      Теорема. Если функция (4.6.2) дифференцируема в точке  и  функция (4.6.1) дифференцируема в соответствующей точке   то сложная функция (4.6.3) дифференцируема в точке .

      Доказательство. По условию дифференцируемости функции  (4.6.2) в точке  ее приращение  Dx(t₀) в этой точке имеет вид:

Dx(t₀) =BDt + a(Dt)Dt,                       (4.8.4)

а приращение Dy(x₀) дифференцируемой функции (4.6.1) в точке x₀  имеет вид:                 

Dy(x₀) = А Dx + a(Dx)Dx.                      (4.8.5)

Функция x = g(t)  дифференцируема в точке   t₀, поэтому непрерывна в этой точке и

lim Dx(t₀) = 0.

      Подставим выражение (4.6.4) в формулу (4.6.5):

Dy(t₀)=А(B Dt+a(Dt)Dt) + a(BDt+a(Dt)Dt)(BDt+a(Dt)Dt).

      Учитывая свойства операций над матрицами [6]  и свойства бесконечно малых функций [5], последнюю формулу можно переписать короче:

Dy(t₀) = CDt + g(Dt) Dt ,                         (4.8.6)

где          C_{n´ l}= A_{m´ n}B_{n´ l},                                                        (4.8.7)

              lim g_{n´ l} (t₀) = 0, 

а это и означает, что сложная функция (4.8.3) дифференцируема в точке t₀, что и требовалось доказать.

      Матрица C= размера  m´l , равная произведению матриц  A_{m´ n}B_{n´ l},  имеет элементы, определяемые формулами

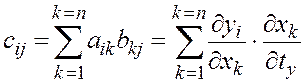 , i=1,2,…, m, j =1,2,…, l.         (4.8.8)

      Рассмотрим частные случаи, относящиеся к числовой функции нескольких переменных  (m = 1).

1.    где  – дифференцируемые функции в точке , а функция  дифференцируема  в соответствующей точке . В этом случае для сложной функции  в соответствии с формулой (5.6.8) имеем

,

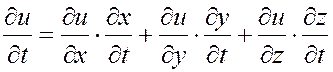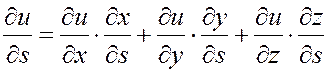.                  (4.8.9)

2.    где  – дифференцируемые функции в точке , а функция  – дифференцируема  в соответствующей точке . В этом случае производная сложной функции  одного аргумента tопределяется формулой

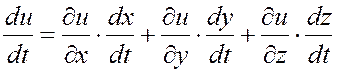.                (4.8.10)

3.    где  – дифференцируемые функции в точке , а функция  – дифференцируема  в соответствующей точке . Это частный случай формулы (4.6.10), когда t = x. Производная сложной функции  одного аргумента x имеет вид:

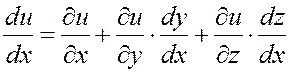.                  (4.8.11)

      Обратите внимание на символы дифференцирования  “” и “”  в формулах (4.8.9), (4.8.10) и (4.8.11). В третьем случае производную , определяемую формулой (4.8.11), называют полной производной  (в отличие от частной производной ).

      П р и м е р ы.

1. 

2. 

      Скорость изменения функции в направлении координатных осей определяется частными производными этой функции по соответствующим переменным.

      В приложениях (например, в экономике и в физике) представляет интерес скорость изменения функции в некотором интересующем исследователя направлении, необязательно совпадающем с направлением координатных осей. Это задача о скорости изменения скалярного поля в заданном направлении.