Дифференцируемость функции. Частное приращение, частный дифференциал и частная производная, страница 2

Df(x₀) =  АDx^T  +  a(Dx) Dx,                        (4.3.1)

где   А = (а₁,  а₂, . . . , а_n) – матрица-строка,

      Dx^T = (Dx₁, Dx₂, . . . ,  Dx_n)^Т – матрица-столбец,

a(Dx) =  (a₁(Dx), a₂(Dx), … , a_n(Dx)) – матрица-строка и 

     a(Dx) = 0,    Dx® 0.                                                                                                                                                                                    

      Элементы матрицы А называются частными производными функции f(x)  в точке x₀. Ниже мы приведем конструктивное определение частных производных, позволяющее сформулировать правило для их вычисления.

      В координатной форме приращение дифференцируемой функции (3.2.1) представим так:

Df(x₀) = (а₁, а₂, . . . , а_n) (Dx₁, Dx₂, . . . ,  Dx_n)^Т +  a(Dx) Dx.

      Произведение   a(Dx) Dxесть числовая функция аргумента Dx. Легко убедиться [5], что эта функция есть бесконечно малая более высокого порядка по сравнению с нормой матрицы Dx:

a(Dx) Dx= o(║Dx║),

где   ║Dx║=.

Поэтому приращение функции имеет вид:

Df(x₀) = а₁ Dx₁ + а₂ Dx₂ + . . . + а_n Dx_n + o(║Dx║).           (4.3.2)

      В соответствии с определением (4.1.4) дифференциал числовой функции в точке x₀ определяется формулой:

df(x₀) = а₁ Dx₁ + а₂ Dx₂ + . . . + а_n Dx_n.                  (4.3.3)

Однако нам все еще неизвестно, как вычисляются элементы  матрицы А = (а₁,  а₂, . . . , а_n).

4.4.  Частное приращение, частный дифференциал

и частная производная

В приращении аргумента  Dx = (Dx₁, Dx₂, . . . ,  Dx_n)^Т положим все приращения аргументов равными нулю, кроме приращения с номером k: Dx_k ¹ 0. Соответствующее приращение функции обозначим f(x₀) и назовем частным приращением функции по аргументу x_k, а соответствующий дифференциал обозначим  и назовем частным дифференциалом по аргументу x_k.  В соответствии с формулами (4.3.2) и (4.3.3) имеем:

= а_k Dx_k + o(Dx_k),                              (4.4.1)

 = а_k Dx_k.                                     (4.4.2)

Здесь k может принимать последовательно все значения от 1 до n.

П р и м е р ы.

1.  Для функции двух переменных найдем частные приращения   по каждой переменной и полное приращение  в произвольной точке  для приращений аргументов :

     ,   , 

2.  Вычислим частное приращение функции  u=   по аргументу  yвточке  (1, 1), соответствующее приращению   ,  и частный дифференциал  d_yu  в этой точке для того же приращения .

 –  =

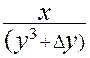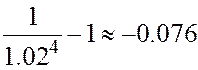
d_yu  =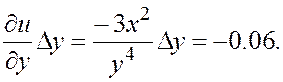 

      Остановимся подробнее на числовой функции трех переменных:

                                   (4.4.3)

которая определена в окрестности точки (x₀, y₀, z₀). Частные приращения этой функции в данной точке, соответствующие приращениям аргументов , определяются формулами:

D_x f(x₀, y₀, z₀) = f(x₀+Dx, y₀, z₀) – f(x₀, y₀, z₀),  

D_y f(x₀, y₀, z₀) = f(x₀, y₀+Dy, z₀) – f(x₀, y₀, z₀),

D_z f(x₀, y₀, z₀) = f(x₀, y₀, z₀+Dz) – f(x₀, y₀, z₀).        (4.4.4)

      Для дифференцируемой функции  (4.4.3), как следует из определения (4.1.1), справедливы формулы:

                          D_x f(x₀, y₀, z₀) = a₁Dx + o(Dx), 

                          D_y f(x₀, y₀, z₀) = a₂Dx + o(Dy), 

  D_z f(x₀, y₀, z₀) = a₃Dx + o(Dz),                       (4.4.5)

где частные производные  a₁, a₂, a₃ не зависят от  Dx,Dy, Dz.Для их определения  делим   D_x f(x₀, y₀, z₀),   D_y f(x₀, y₀, z₀),  D_z f(x₀, y₀, z₀)  соответственно  на   Dx, Dy,  Dz и переходим к пределу:

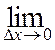
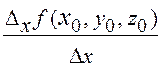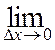
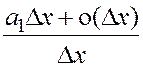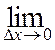
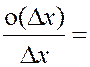 =    =  a₁+a₁.

Аналогично получаем a₂ иa₃. Обозначая частные производные соответственно 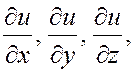     приходим к формулам, определяющим частные производные:

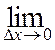
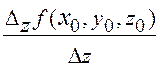                                      =.                          (4.4.6)

      Полный дифференциал (4.3.3.) функции можно представить теперь в виде

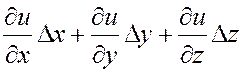,                              (4.4.7)

а для полного приращения дифференцируемой функции справедлива формула:

 +

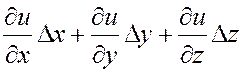+ о       (4.4.8)