Министерство образования Республики Беларусь
Учреждение образования «Гомельский государственный
технический университет имени П.О.Сухого»
Кафедра «Высшая математика»
В.И. Гойко, В.Г. Тепляков
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ И ЭЛЕМЕНТЫ
ЛИНЕЙНОЙ АЛГЕБРЫ
лекции
по курсу «Высшая математика» и «Математика»
для студентов заочного отделения всех специальностей
Гомель 2010
УДК 517.37
ББК
Рекомендовано к изданию научно-методическим советом факультета автоматизированных и информационных систем
ГГТУ им. П.О.Сухого
(протокол № ____ от __________________)
Рецензент: зав. кафедрой «Высшая математика» УО БелГУТ, канд. физ.-мат. наук, доцент С.П. Новиков.
Гойко В.И.
Аналитическая геометрия и элементы линейной алгебры. Пособие по курсу «Высшая математика» для студентов заочного отделения всех специальностей / В.И. Гойко, В.Г. Тепляков. – Гомель: ГГТУ им. П.О.Сухого, 2010. – с.
В пособии излагаются основы аналитической геометрии и элементы линейной алгебры. Приводится достаточно большое количество решенных задач и примеров, иллюстрирующих основные положения, формулы и определения аналитической геометрии и линейной алгебры.
Для студентов всех специальностей заочного отделения технических университетов.
Глава 1
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ
Рассмотрим на прямой ![]() две различные точки Oи E.
Будем говорить, что точка Mпрямой
две различные точки Oи E.
Будем говорить, что точка Mпрямой ![]() , отличная от точки O, и точка E
лежат по одну сторону относительно O, если
точка O не лежит между E и M.
Точки E и M лежат по разные стороны от точки O,
если O лежит между ними.
, отличная от точки O, и точка E
лежат по одну сторону относительно O, если
точка O не лежит между E и M.
Точки E и M лежат по разные стороны от точки O,
если O лежит между ними.
Лучом (O,
E) называется совокупность точек, состоящую из O,
E и всех точек M прямой ![]() , лежащих по одну сторону с точкой E
относительно точки O. Точка O называется началом
луча.
, лежащих по одну сторону с точкой E
относительно точки O. Точка O называется началом
луча.
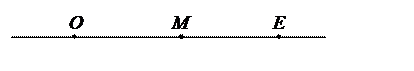
Рассмотрим на прямой ![]() две точки O иE.
Точка O делит прямую
две точки O иE.
Точка O делит прямую ![]() на
два луча. Точка O называется началом системы координат, прямая
на
два луча. Точка O называется началом системы координат, прямая
![]() – осью координат. Выберем отрезок OE
в качестве единицы масштаба. Возьмем на прямой
– осью координат. Выберем отрезок OE
в качестве единицы масштаба. Возьмем на прямой ![]() произвольную точку M. Этой
точке поставим в соответствие число x,
определяемое следующим образом:
произвольную точку M. Этой
точке поставим в соответствие число x,
определяемое следующим образом:
1)
![]() – длина
отрезка OM, измеренного
при помощи единичного отрезка OE;
– длина
отрезка OM, измеренного
при помощи единичного отрезка OE;
2)
![]() , если
точки MиE
принадлежат одному лучу ( O, E) и
, если
точки MиE
принадлежат одному лучу ( O, E) и ![]() , если точки MиE принадлежат разным лучам
прямой
, если точки MиE принадлежат разным лучам
прямой ![]() относительно
точки O;
относительно
точки O;
3)
![]() , если
точка M совпадает с точкой O.
, если
точка M совпадает с точкой O.
Число
x называется координатой точки M
и записывается так: M(x).
Обратно, всякому числу x ставится в соответствие на прямой ![]() точка M, для которой число x
есть координата, если даны начало системы координат O
и единица масштаба OE.
точка M, для которой число x
есть координата, если даны начало системы координат O
и единица масштаба OE.
§1. Вычисление длины отрезка на прямой. Деление отрезка в данном отношении
Пусть даны две точки ![]() и
и ![]() .
.
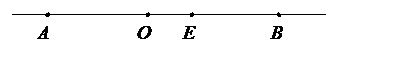
Длина отрезка AB, измеренного единичным отрезком OE, вычисляется по формуле:
![]() (1.1)
(1.1)
Разделить отрезок в данном отношении l – это значит на прямой AB найти такую точку C, что выполняются следующие условия:
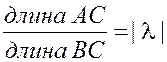 ;
;
точка C
принадлежит отрезку AB, если ![]() , и лежит вне отрезка
AB, если
, и лежит вне отрезка
AB, если ![]() .
.
Пусть координаты точек A и B
будут соответственно ![]() и
и ![]() . Так
как
. Так
как ![]() ,
, ![]() , а знаки разностей
, а знаки разностей ![]() и
и ![]() одинаковы,
если точка C принадлежит
отрезку AB, и различны в противном случае, то получим равенство:
одинаковы,
если точка C принадлежит
отрезку AB, и различны в противном случае, то получим равенство:
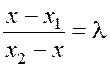 .
.
Теперь получаем: ![]() . Если
. Если ![]() , то
, то ![]() .
.
Если ![]() , то
, то ![]() . В этом случае делящая точка C(x)
будет серединой отрезка.
. В этом случае делящая точка C(x)
будет серединой отрезка.
§ 2. Прямоугольные декартовы координаты на плоскости
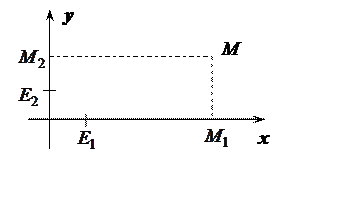
Рассмотрим на плоскости две взаимно перпендикулярные прямые. Пусть точка O – точка пересечения этих прямых и E1, E2 – две точки на этих прямых, удовлетворяющих условию:
![]() . Точка
O называется
началом системы координат, ось Oxназывается осью абсцисс,
ось Oy – осью ординат. На рисунках ось абсцисс
проводится горизонтально, а ось ординат – вертикально. На оси абсцисс
положительным направлением считается направление слева направо, а на оси
ординат положительным направлением считается направление снизу вверх.
. Точка
O называется
началом системы координат, ось Oxназывается осью абсцисс,
ось Oy – осью ординат. На рисунках ось абсцисс
проводится горизонтально, а ось ординат – вертикально. На оси абсцисс
положительным направлением считается направление слева направо, а на оси
ординат положительным направлением считается направление снизу вверх.
Пусть M
– произвольная точка плоскости. Проведем
перпендикуляры из точки M к осям Oxи Oy и найдем точки ![]() и
и ![]() пересечения этих
перпендикуляров с соответствующими осями. Координатами точки M
называются числа
пересечения этих
перпендикуляров с соответствующими осями. Координатами точки M
называются числа ![]() ,
, ![]() . Запись
. Запись ![]() обозначает,
что
обозначает,
что ![]() ,
, ![]() есть
координаты точки M. Теперь мы скажем, что на плоскости построена декартова
прямоугольная система координат, которая обозначается символом Oxy.
Каждой точке M плоскости
поставлена в соответствие вполне определенная пара вещественных чисел, взятых в
определенном порядке, короче, упорядоченная пара чисел – ее координаты x
и y. Обратно, каждой упорядоченной паре действительных
чисел x и y соответствует единственная точка M,
координаты которой равны x и y.
есть
координаты точки M. Теперь мы скажем, что на плоскости построена декартова
прямоугольная система координат, которая обозначается символом Oxy.
Каждой точке M плоскости
поставлена в соответствие вполне определенная пара вещественных чисел, взятых в
определенном порядке, короче, упорядоченная пара чисел – ее координаты x
и y. Обратно, каждой упорядоченной паре действительных
чисел x и y соответствует единственная точка M,
координаты которой равны x и y.
§ 3. Вычисление длины отрезка на плоскости
Вычислим длину d отрезка AB, если заданы координаты точек ![]() и
и ![]() . Проведем
через точки Aи
B прямые,
параллельные осям координат, до пересечения с ними в точках
. Проведем
через точки Aи
B прямые,
параллельные осям координат, до пересечения с ними в точках ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Рассмотрим прямоугольный треугольник ![]() . Используя теорему Пифагора, получим:
. Используя теорему Пифагора, получим:
![]() ,
,
![]() .
.
Отсюда получаем следующую формулу:
![]() (1.2)
(1.2)
Если прямая AB
параллельна одной из осей координат, например,
оси Ox, или совпадает с ней, то длина отрезка ABравна длине отрезка ![]() . Следовательно,
. Следовательно, ![]() и так как в этом случае
и так как в этом случае ![]() , то d вычисляется по формуле
(1.2). Формула (1.2) является общей формулой, справедливой для любого положения
точек A, B на плоскости.
, то d вычисляется по формуле
(1.2). Формула (1.2) является общей формулой, справедливой для любого положения
точек A, B на плоскости.
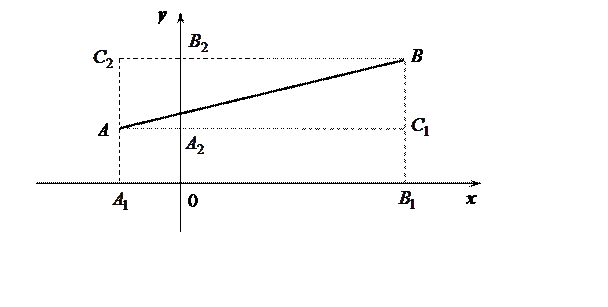
Пример 3.1. Вычислить длину отрезка AB,
если ![]() ,
, ![]() .
.
Решение. Используем формулу (1.2):
![]() .
.
§ 4. Деление отрезка в данном отношении
Пусть даны точки ![]() ,
, ![]() . Требуется найти точку
. Требуется найти точку ![]() , которая делит отрезок
, которая делит отрезок ![]() в отношении l1 : l2, т. е.
удовлетворяющую соотношению
в отношении l1 : l2, т. е.
удовлетворяющую соотношению
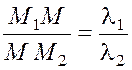 . Тогда координаты точки
. Тогда координаты точки ![]() вычисляются по формулам:
вычисляются по формулам:
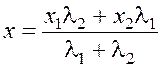 ,
, 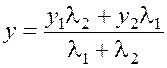 . (1.3)
. (1.3)
Пусть ![]() – середина
отрезка M1M2. Легко видно, что координаты точки
– середина
отрезка M1M2. Легко видно, что координаты точки ![]() вычисляются по следующим формулам:
вычисляются по следующим формулам:
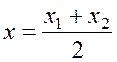 ,
, 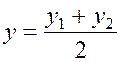 . (1.4)
. (1.4)
Пример 4.2.
Найти центр тяжести ![]() треугольника
треугольника ![]() , если
, если ![]() .
.
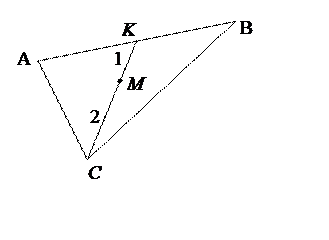 Решение. Известно, что искомая точка
Решение. Известно, что искомая точка ![]() лежит
на пересечении медиан треугольника и делит каждую из них в отношении
лежит
на пересечении медиан треугольника и делит каждую из них в отношении ![]() (считая от вершины треугольника). Т.к. CK– медиана,
то
(считая от вершины треугольника). Т.к. CK– медиана,
то ![]() – середина
стороны
– середина
стороны ![]() . Тогда
. Тогда 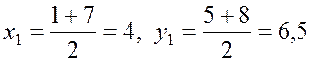 . Теперь
используем формулы (1.3). Делим отрезок
. Теперь
используем формулы (1.3). Делим отрезок ![]() в
отношении
в
отношении ![]() , получим:
, получим: 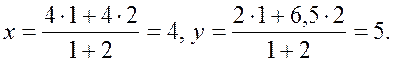 Итак, M(4; 5).
Итак, M(4; 5).
§ 5. Полярные координаты точки
Рассмотрим на плоскости луч (O, E) с начальной точкой O и некоторой точкой E. Луч называется полярной осью, точка O – полюсом, точка E – единичной точкой.
 Пусть M – произвольная точка
плоскости. Длину отрезка OM, измеренного единичным отрезком OE,
называют длиной полярного радиуса точки M и
обозначают r. Положительный угол от луча (O,
E) до луча (O, M)
называют полярным углом точки M и
обозначают буквой φ. Пара чисел φ и r
называется полярными координатами точки M. Последний
факт записывается следующим образом: M(φ, r).
Пусть M – произвольная точка
плоскости. Длину отрезка OM, измеренного единичным отрезком OE,
называют длиной полярного радиуса точки M и
обозначают r. Положительный угол от луча (O,
E) до луча (O, M)
называют полярным углом точки M и
обозначают буквой φ. Пара чисел φ и r
называется полярными координатами точки M. Последний
факт записывается следующим образом: M(φ, r).
Если известны полярные координаты φ, r точки M, то по формулам:
![]() ;
; ![]() (1.5)
(1.5)
вычисляются декартовы координаты. Обратно, если известны декартовы координаты x,y точки M, то ее полярные координаты вычисляются по формулам:
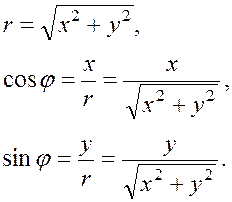 (1.6)
(1.6)
§ 6. Элементы векторной алгебры
Одни физические величины такие, как масса, температура, время можно вполне характеризовать заданием их численного значения. Такие величины называются скалярными, а числа, выражающие значения этих величин, называются скалярами. Другие же величины такие, как сила, скорость, ускорение характеризуются
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.