Математический аппарат радиотехники. Часть II. Случайные процессы: Учебное пособие, страница 4

Если же хотя бы один из аргументов ФР равен , то она равна нулю, так как произведение случайных событий, одно из которых, , является невозможным событием. Как и одномерная, многомерная ФР является неубывающей функцией по каждому из аргументов.

Аналогично одномерному случаю, определяется непрерывный случайный вектор (непрерывная многомерная СВ), если существует неотрицательная функция  такая, что при любых

=,

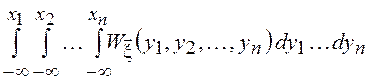и =.

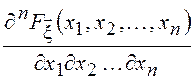При использовании обобщенных функций понятие ПВ можно распространить и на дискретные многомерные СВ. Как и одномерная, многомерная ПВ удовлетворяет условию нормировки

.

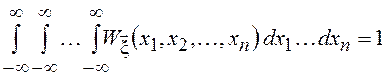Если многомерную ПВ проинтегрировать по всем значениям одной из переменных, то получим ПВ остальных СВ, т. е.

.

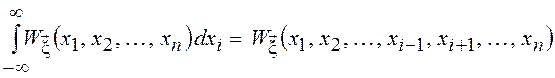Данное свойство часто называют условием согласованности.

Для ФР это эквивалентно тому, что мы положили . Эти свойства называются согласованностью высших и низших ФР и ПВ. Вероятность попадания точки () в область G равна

.

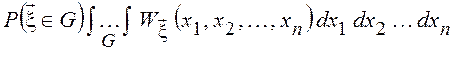Как и для случайных событий, для случайных величин можно определить понятие зависимости. Говорят, что СВ  являются зависимыми, если ПВ одной из них зависит от того, какое значение приняла другая СВ. Это записывается при помощи условной ПВ случайной величины , что читается как условная ПВ случайной величины  при условии, что СВ  приняла значение .

Если ПВ случайной величины  или   не зависит от того, какое значение приняла другая величина, то такие СВ называются независимыми.

В общем случае совместная ПВ случайных величин  и   записывается в виде

= = .

Для независимых СВ = , что можно рассматривать как условие независимости СВ.

Для многомерных СВ эти формулы примут вид

 =   =

= = = 

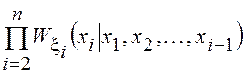
и для независимых СВ =.

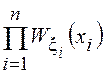Определение независимых СВ на языке ФР звучит так: если для любой совокупности исходных случайных величин , где  имеет место равенство

,

то СВ  независимы.

Условные плотности вероятностей обладают всеми свойствами ПВ. Они неотрицательны, т.е.  и выполняется условие нормировки 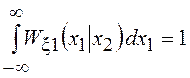 при любых значениях .

Пример. Многомерное нормальное распределение. Многомерная случайная величина = подчиняется нормальному распределению, или  - нормальный случайный вектор, если

=,

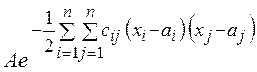где 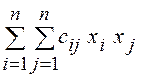 - положительно определенная квадратичная форма, пол-ностью заданная своей матрицей С=, ,  - константа, определяемая из условия нормировки 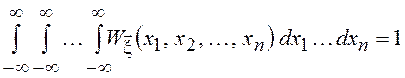. Структура матрицы С будет определена чуть позднее.

Контрольные вопросы

1. Дайте определение случайной величины.

2. Для случайной величины , принимающей значения 0,1; 0,2; 0,4; 0,6 с вероятностями 0,3; 0,2; 0,2; 0,3 соответственно, построить многоугольник распределения.

3. Что такое функция распределения СВ? Какие свойства ФР вам известны? Постройте ФР для случайной величины , определенной в предыдущем вопросе.

4. Дайте определение непрерывной СВ. Что такое плотность вероятности? Каковы ее свойства?

5. Приведите выражение для ФР и ПВ случайной величины  из п. 2.

6. Как определяется СВ, подчиняющаяся распределению Бернулли?

7. Как определяется СВ, подчиняющаяся биномиальному распределению?

8. Дайте определение СВ, значения которой равномерно распределены на интервале . Постройте ПВ и ФР равномерно распределенной на промежутке  СВ .

9. Запишите выражения для ПВ и ФР нормальной СВ.

10. Сформулируйте локальную предельную теорему.

11. Как звучит интегральная теорема Муавра–Лапласа?

12. Что такое многомерная или векторная СВ?

13. Как определяется ФР многомерной СВ?

14. Что такое непрерывный случайный вектор? Как для него определяется ПВ? Как связаны ПВ и ФР непрерывного случайного вектора?

15. Что такое условная плотность вероятности? Каковы ее свойства?

16. Запишите совместную ПВ СВ  и   для двух случаев: когда   и   являются зависимыми и независимыми СВ.

17. Считая  и   независимыми нормальными СВ с параметрами , , и ,  соответственно. Найти вероятность попадания точки с координатами  и   в прямоугольник, вершины которого располагаются в точках (1,2); (3,2); (1,4); (3,4). Полагая  =  = 2, и  =  = 16, найдите значение искомой вероятности.