Физика \ Физика

Исследование вынужденных колебаний в колебательном контуре (лабораторная работа), страница 2

ВВЕДЕНИЕ

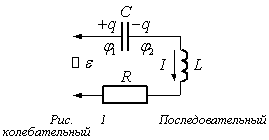
1. Чтобы в колебательном контуре, электрическая схема которого представлена на рис.1, совершились вынужденные колебания, необходимо включить последовательно с элементами контура генератор – источник ЭДС.  ε:

                                   (1)

По закону Ома для неоднородного участка цепи имеем для контура (потенциал обкладок и направление тока показаны на рис. 1; направление обхода – по часовой стрелке):

                                            ,                                  (2)

где  – ЭДС самоиндукции; активное сопротивление катушки индуктивности включено в R; внутренним сопротивлением генератора пренебрегаем.

Пусть  q – заряд на обкладках конденсатора, тогда:   ;     и получаем уравнение вынужденных колебаний:

                                                              (3)

Обозначая              ,       ,                                         (4)

где   ω0 – собственная частота контура,  β  – коэффициент затухания, получаем:

                                                                              (5)

(точка – дифференцирование по времени).

Уравнение (5) является неоднородным линейным дифференциальным уравнением второго порядка. Такого типа уравнения описывают поведение широкого класса колебательных систем (электрических, механических) под влиянием внешнего синусоидального воздействия.

Общее решение уравнения (5) складывается из общего решения q1 однородного уравнения:

                                                                             (6)

и частного решения неоднородного уравнения (5). Общее решение однородного уравнения (6), в случае слабого затухания , описывает собственные затухающие колебания:

                                    ,                                    (7)

где  – амплитуда колебаний;  – циклическая частота затухающих колебаний. Константы А и α из начальных условий.

Частное решение уравнения (5) проще всего искать в комплексной форме, сделав замену в правой части .

Правая часть уравнения (5) пропорциональна действительной части этого выражения. Пусть решением нового уравнения является комплексная функция , так что                                                                                                                  (8)

Тогда действительная часть этой функции  является решением уравнения, у которого в правой части стоит   т.е, искомым решением уравнения (5).

Будем искать частное решение уравнения (8) в виде . Подставляя это выражение в уравнение (8) получим:  , тогда

.

Скачать файл