Импульсные и дискретные системы, страница 2

          Решетчатая функция определена выражением (8.1). При таком определении размерность решетчатой функции x^*(t) не совпадает с размерностью непрерывного сигнала x(t) (размерность δ-функции обратная размерности ее аргумента). По этой причине иногда выполняют нормировку: i=t_i/Δt и определяют решетчатую функцию так:

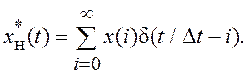
          Выборочные значения непрерывного сигнала x(t) (x(t_i) или x(i)) называют дискретной функцией. Для описания динамики дискретной  функции во временной области используются разностные уравнения (разностные уравнения в векторной рекуррентной форме использовались в предыдущих разделах).

          Применим к (8.1) преобразование Лапласа:

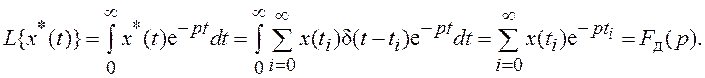        (8.2)               

          Полученное выражение (8.2) известно как дискретное преобразование Лапласа, определяющее изображение F_д(p) для дискретной функции x(t_i). Если в (8.2) выполнить замену p=jω, то получим спектр решетчатой функции F_д(jω). Функция  периодичная (период равен 2π/Δt), поэтому спектр решетчатой функции представляет собой бесконечный ряд сдвинутых копий спектра непрерывного сигнала x(t) (рис. 8.3). Очевидно, что восстановление сигнала x(t) по решетчатой функции x^*(t) возможно с помощью идеального фильтра нижних частот, выделяющего «основной спектр», только в том случае, если «дополнительные спектры» не накладываются на «основной спектр» (2ω_м<2π/Δt – условие теоремы Котельникова).

          Изображение F_д(p) дискретного преобразования Лапласа содержит трансцендентную функцию переменной p. Удобнее использовать z-преобразование. Для этого вводится обозначение  и выражение (8.2) принимает вид:

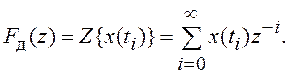                                   (8.3)

          Заметим, что z-преобразование может быть записано также для непрерывного сигнала: Z{x(t)}. Такая форма записи означает, что непрерывный сигнал x(t) заменяется дискретной функцией x(t_i) и, далее, к ней применяется z-преобразование.

          В некоторых случаях оказывается полезной смещенная решетчатая функция (δ-импульсы смещаются на величину δτ относительно моментов времени t_i). При этом указывается дополнительный аргумент ε: x^*(t, ε). Этот аргумент характеризует относительный сдвиг ε=δτ/Δt  δ-импульсов на интервале временной дискретизации . Полезность смещенной решетчатой функции покажем на следующем примере. Рассмотрим непрерывный сигнал x(t)=1+Asin2πft. При выборе t_i=i/2f дискретная функция x(t_i)=1 не отражает поведения x(t) внутри интервала временной дискретизации Δt=1/2f.  Полностью описать поведение x(t) можно с помощью смещенной решетчатой функции x^*(t, ε), при этом соответствующая ей дискретная функция имеет вид: x(t_i, ε)= 1+(-1)ⁱAsinπε.

          Для смещенной решетчатой функции вводят модифицированное z-преобразование:

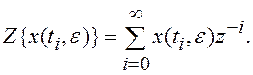                                        (8.4)

          Ряд (8.4) удается просуммировать во многих случаях, однако удобнее для нахождения z-преобразования использовать готовые результаты, обычно представленные в виде таблиц. В качестве примера в табл. 8.1 приведены преобразования Лапласа и z-преобразования для ступенчатой x(t)=1(t) и линейной x(t)=t функций.

Таблица. 8.1.

          Таблицы такого вида полезны также для нахождения преобразования Z{x(t)} при известном преобразовании L{x(t)}.

8.3. Передаточная функция дискретной системы

          Рассмотрим дискретную систему со скалярным воздействием g(t_i) и реакцией y(t_i). Пусть система описывается разностным уравнением

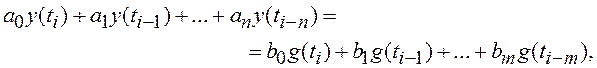      (8.5)

где a₀,…,a_n и b₀,…,b_m – постоянные коэффициенты; начальные условия полагаем нулевыми.

          Применяем к уравнению (8.5) z-преобразование:

где y(z) и g(z) – z-преобразования для y(t_i) и, соответственно, g(t_i).

          Определим ПФ дискретной системы как отношение z-преобразований реакции системы и воздействия: