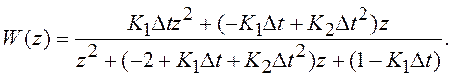Импульсные и дискретные системы, страница 5

 В этом случае ПФ системы в разомкнутом состоянии равна 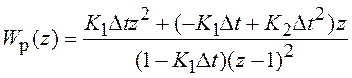 и проявляются свойства системы 2-го порядка астатизма. Частотная ПФ системы в этом случае (при ω<<2π/Δt ) имеет вид: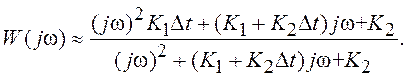

Пример 2. С помощью билинейного преобразования найдем ПФ дискретной системы, эквивалентной непрерывной с ПФ в замкнутом состоянии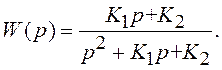  

Подстановка 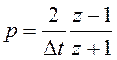 приводит к результату:

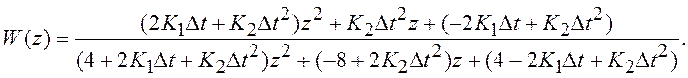
 Получили более сложную в реализации дискретную систему. Применение алгебраического критерия устойчивости (см. разд. 2.6) показывает, что условия устойчивости этой дискретной системы полностью совпадают с условиями устойчивости непрерывной системы: K₁>0, K₂>0.

8.4. Передаточная функция дискретно-непрерывной системы

          Рассматривается система, содержащая ИИЭ, фиксатор нулевого порядка (ФНП) и непрерывную часть с ПФ W_н(p) (рис. 8.4).

          Для описания непрерывного сигнала y(t) можно использовать смещенную решетчатую функцию, которой соответствует дискретная функция y(t_i, ε). Пусть y(z, ε) – модифицированное z-преобразование функции y(t_i, ε), а g(z) - z-преобразование воздействия g(t). Определим ПФ системы:

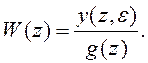                                                    (8.12)

          ФНП совместно с непрерывной частью с ПФ W_н(p) называют приведенной непрерывной частью системы с ПФ:

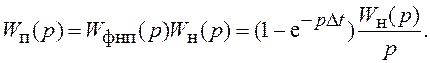                 (8.13)

          В уравнении (8.13) функцию передачи интегратора, содержащегося в ФНП, относят к ПФ W_н(p) и для ПФ W_н(p)/p по таблицам (вида табл. 8.1) находят z-преобразование W_н(z,ε). Для первого сомножителя в (8.13) z-преобразование записывается естественным образом: 1-z^-1. В результате определяется z-преобразование для приведенной непрерывной частью системы:

                                    (8.14)

          Выражение для сигнала рассогласования x(t) в дискретные моменты времени t_i запишем так, чтобы учесть конечное быстродействие элементов системы, не позволяющее отрабатывать сигнал рассогласования мгновенно:

                                    (8.15)

          Применяем к (8.15) z-преобразование:

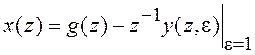                                    (8.16)

и учитываем соотношение

                                            (8.17)

          С помощью уравнений (8.16) и (8.17), с учетом (8.12), получаем общее выражение для ПФ рассматриваемой системы:

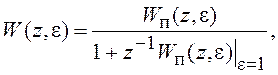                                 (8.18)

где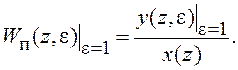

          В частном случае, когда   (нет скачков), вместо (8.18) возможно использование выражения

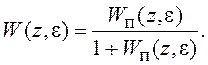                                  (8.19)

Если W_п(z,ε) в (8.19) рассматривать как ПФ разомкнутой системы, то выражение (8.19) аналогично соотношению (1.4) для непрерывной системы.

          В качестве примера найдем ПФ дискретно-непрерывной системы с W_н(p)=K/p. С помощью табл. 8.1 определяем

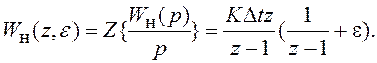
В соответствии с (8.14)

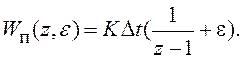
Если интересоваться только дискретными значениями y(t_i), то ПФ системы равна 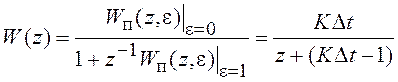 и совпадает с ПФ дискретной системы, рассмотренной в разд. 8.3 (пример 1).

8.5. Анализ систем с конечным временем съема данных

          Рассматриваются системы, содержащие ИЭ (линейный ключ), причем время замыкания ключа Δτ соизмеримо с периодом Δt (рис. 8.1). Следует отметить две основные особенности таких систем:

- это системы с переменными параметрами и, поэтому, анализ их следует выполнять во временной области;

- периодическая работа ключа в системах 2-го порядка и выше вызывает проблемы, связанные с обеспечением устойчивости и требуемого качества переходных процессов.

          Сначала рассмотрим особенности анализа систем с конечным временем съема данных и последующей непрерывной обработкой сигнала. Пусть структура системы согласована с некоторым формирующим фильтром (см. разд. 1.11) и представлена в виде, показанном на рис. 8.5. 

          Коэффициент K(t) изменяется в зависимости от состояния ключа:

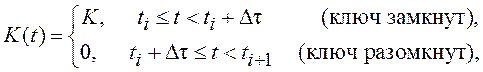
где t_i=iΔt,   i=0,1,2,… - моменты замыкания ключа.

          Динамика вектора состояния системы описывается векторными дифференциальными уравнениями: