Евклидово пространство. Использование неравенства Коши–Буняковского, страница 4

Преимущество ортогональных базисов состоит в том, что для отыскания координат вектора в ортогональном базисе нет необходимости решать линейную систему уравнений. Для ортогонального базиса  координаты вектора, принадлежащего L₂ (для функции  f(t)  коэффициенты Фурье), равны:

.

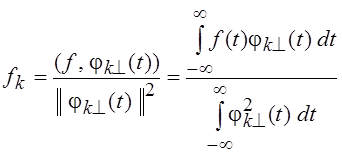В этой связи актуальной является задача построения на основе линейно независимой системы векторов эквивалентной ей ортогональной системы. Такую возможность дает процедура Грама–Шмидта.

Пусть  – система линейно независимых векторов и нам надо построить ортогональную систему, каждый вектор которой был бы линейной комбинацией векторов системы .

Выберем в качестве первого вектора новой системы  первый вектор исходной, т. е. _1^ = ₁. Второй вектор ортогональной системы построим как _2^ = l_211^ + ₂, где коэффициент l₂₁ выбирается из условия ортогональности _1^ и _2^, т. е. (_1^, _2^) = 0 = l₂₁(_1^, _1^) + (₂, _1^), откуда 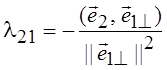. Третий вектор _3^ строится как сумма линейной комбинации _1^ и _2^ и третьего вектора исходной системы:

_3^ = l_322^ + l_311^ + ₃.

Учитывая ортогональность _1^ и _2^, а также условие ортогональности _3^ двум построенным векторам _1^ и _2^, получим:

; .

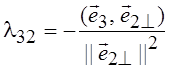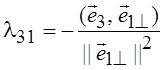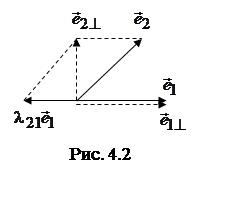
Таким образом, в основе процедуры лежит следующая схема: 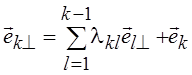, где 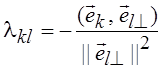. Иллюстрация этой процедуры для R₂ (плоскости) приведена на рис. 4.2.

Поясним описанную процедуру с помощью нескольких примеров.

1.  Система функций вида , t ³ 0, где k = 1, 2, … – номер функции, с > 0 – масштабный множитель, является линейно независимой,
так как заменой  сводится к линейно независимой системе ,
k = 1, 2, …, с которой мы уже встречались.

Ортогональная система на промежутке [0, ¥) в соответствии с процедурой Грама–Шмидта строится следующим образом. Первая функция ; вторая , где 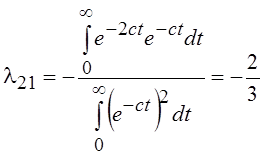, таким образом 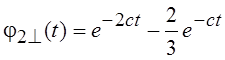. Такая система используется для аппроксимации корреляционных функций стационарных случайных процессов, о которых пойдет речь в гл.7.

2.  Полиномы Лежандра.

Полиномы Лежандра P_k(t) получаются на основе ортогонализации на промежутке [–1, 1] системы линейно независимых функций . Каждая функция ортогональной системы, строящейся на основе , будет линейной комбинацией степеней t, т. е. P_k(t) = 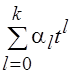, что представляет собой полином. В соответствии с процедурой Грама–Шмидта P₀(t) = t⁰ = 1;

P₁(t) = l₁₀ P₀(t) + t, где 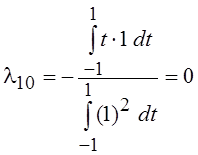, т. е. P₁(t) = t;

P₂(t) = l₂₁ P₁(t) + l₂₀ P₀(t) + t²,

где 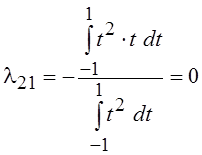, , 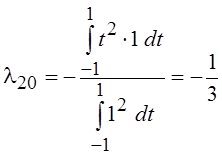т. е. P₂(t) = t² – ;

P₃(t) = l₃₂ P₂(t) + l₃₁ P₁(t) + l₃₀ P₀(t) + t³, где ,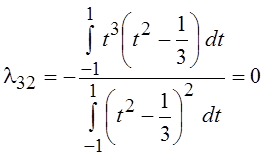

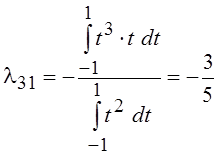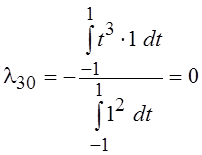, , т. е. P₃(t) = t³ – t.

Построенная система полиномов Лежандра нормирована таким образом, чтобы коэффициент при старшей степени равнялся бы единице. Используют и другие способы нормировки (см. гл.6).

В L₂ [a, b]  можно ввести метрику, учитывающую, в каких точках промежутка [a, b] возникает отклонение функций друг от друга, т. е.

,

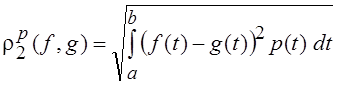где p(t) – весовая функция. Весовая функция должна быть неотрицательной, и для " f(t) Î  интегралы 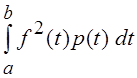 должны сходиться.

Система функций  называется ортогональной на промежутке [a, b] с весом p(t), если

,

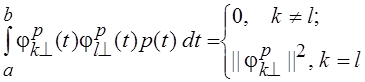где  – квадрат нормы по весу p(t).

Система функций , ортогональная с весом p(t), может быть превращена в просто ортогональную, если рассматривать функции .

Ортогонализация системы линейно независимых функций , k = 0, 1, … на различных промежутках с различными весовыми функциями позволяет построить системы ортогональных полиномов , из которых особую роль играют так называемые классические ортогональные полиномы.

Классическими называют ортогональные полиномы, у которых весовая функция p(t) удовлетворяет дифференциальному уравнению 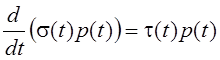, где t(t)  и s(t)  – полиномы степени не выше первой и второй соответственно. Их конкретный вид определяется интервалом ортогональности, который может быть конечным, полубесконечным, или соответствовать всей числовой оси (–¥, ¥). В табл.4.1 приведены основные характеристики классических ортогональных полиномов.

Табл.4.1