Евклидово пространство. Использование неравенства Коши–Буняковского, страница 2

Это – неоднородная система, иначе совокупность векторов  не была бы базисом (продумать самостоятельно), поэтому она имеет решение, если ее определитель G(₁, ₂, …, _n), называемый определителем Грама, отличен от нуля, т. е.

G(₁, ₂, …, _n) = 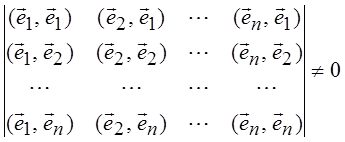.            (4.3)

Можно показать, что определитель Грама имеет смысл квадрата объема гиперпараллелепипеда, натянутого на вектора ₁, ₂, …, _n. Для п = 1 это
(₁, ₁) = ||(₁)||² – квадрат длины вектора ₁; для  п = 2  определитель G(₁, ₂) = || ₁||²||₂||² – |(₁, ₂)|² – квадрат площади параллелограмма, построенного (натянутого) на векторах ₁ и ₂, и т. д. Учитывая сказанное, можно утверждать, что для системы линейно независимых векторов определитель Грама G(₁, ₂, …, _n) > 0. Для системы ненулевых ортогональных векторов  G(_1^, _2^, …, _n^) = .

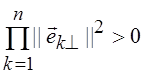Определитель Грама можно записать в форме

G(₁, ₂, …, _n) = G(₁, ₂, …, _{n – 1}),

где  – квадрат нормы вектора  в представлении =+. В этом представлении вектор , называемый проекцией вектора  на подпространство М, натянутое на вектора ₁, ₂, …, _{n – 1}, представляет собой вектор, принадлежащий М и максимально близкий,  в смысле используемой метрики, к вектору , т. е. |||| = , где минимизация ведется по всем векторам , принадлежащим М.

При разложении вектора  по ортогональному базису  квадрат нормы вектора  будет равен

||||² = (,) = .

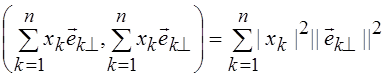Если базисная система ортонормальна  (), то ||||² =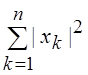. Это соотношение часто называют равенством Парсеваля.

Координаты вектора  относительно ортогонального базиса  равны х_п = 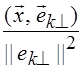, а для ортонормального  х_п = . Читателю предлагается самостоятельно доказать данные утверждения.

С учетом приведенных результатов скалярное произведение в С_п записывается как (, ) =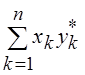, а в R_n  (, ) =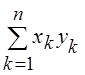, где х_k и y_k – координаты векторов  и  в ортонормальном базисе.

Часто бывает удобным введение базиса , взаимного с базисом . Базис  называется взаимным с базисом , если составляющие его вектора попарно ортогональны с векторами базиса , т. е. , i = 1, 2, …, n, где 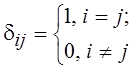 – символ Кронекера.

Если базис  является ортонормальным, то он совпадает со своим взаимным базисом. При использовании взаимных базисов  и  для любого вектора , принадлежащего линейному пространству R_n или С_п, в котором  является базисом, можно записать

.

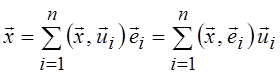Взаимный базис используется при переходе от одного базиса к другому.

Приведем примеры евклидовых пространств и ортогональных базисов в них.

1.  В R_n ортонормальным базисом является введенный выше базис с векторами _1^= (1, 0, …, 0); _2^= (0, 1, …, 0); _n^= (0, 0, …, 1). Его частным случаем для трехмерного пространства R₃ являются орты .

2.  В пространстве L₂ [a, b] скалярное произведение функций f(t) и g(t) определяется как 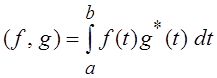, а  в L₂ как .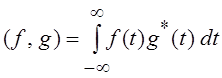

Если L₂ [a, b] или L₂ – вещественные функциональные пространства, то знак комплексного сопряжения “*” опускается.

В L₂ [a, b] используются разнообразные базисы, из которых важнейшим является тригонометрический базис, состоящий из функций 1, 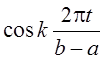, , 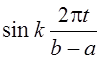k = 1, 2, … . Для промежутка длиной 2p базисной будет система функций 1, cos kt, sin kt. Базисной будет и система , k = 0, ± 1, ± 2, … . Поскольку  = cos kt + j sin kt, т. е.  каждая функция этой системы является линейной комбинацией функций предыдущей, то обе системы эквивалентны.

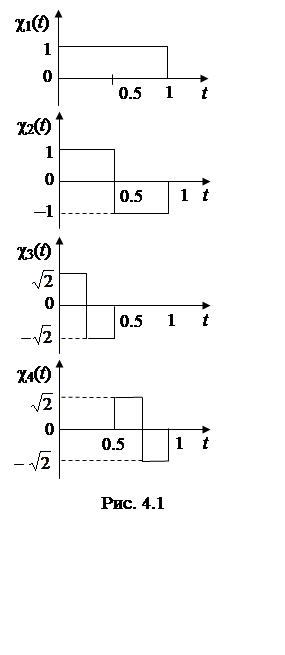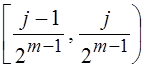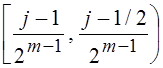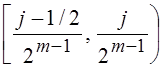Базисные функции не обязательно должны быть непрерывными. Так, в L₂ [0, 1]  можно построить ортонормальную базисную систему функций Хаара, определяемую следующим образом.  Функция Хаара c_mj(t) отлична от нуля на двоичном промежутке , где m = 1, 2, … , а j = 1, 2, …, 2^m-1.  На левой половине двоичного отрезка  функция Хаара c_mj(t) = , а на правой половине  соответственно c_mj(t) = –. Обычно для нумерации функций Хаара используют один индекс
k =  2^{m –1} + j, m = 1, 2, … ; j = 1, 2, …, 2^{m – 1}. При таком обозначении нумерация функций Хаара c_k(t) начинается с k = 2. При этом c₁(t) полагается равной единице на всем промежутке [0, 1]. На рис. 4.1 приведены первые четыре функции Хаара. Более подробное знакомство с функциями Хаара мы отложим до гл. 6, посвященной специальным функциям.