Анализ нелинейных систем. Метод гармонической линеаризации. Применение теории марковских процессов для анализа нелинейных систем, страница 2

          Одним из эффективных методов анализа нелинейных систем является решение дифференциальных уравнений. В качестве иллюстрации рассмотрим поведение нелинейной системы ФАПЧ 1-го порядка в установившемся режиме. Структурная схема системы показана на рис. 7.1. Нелинейным элементом является фазовый дискриминатор, имеющий статическую характеристику вида:  где A - максимальное напряжение на выходе дискриминатора. Величина Δω_н учитывает начальную расстройку частоты управляемого генератора, имеющего коэффициент усиления K_уг (этот коэффициент имеет размерность град/с/в и включает в себя коэффициент усиления варикапа). Система описывается дифференциальным уравнением:

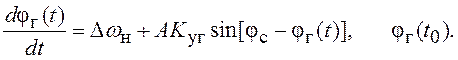
          Нас интересует ошибка в установившемся режиме, поэтому запишем дифференциальное уравнение для ошибки  (полагаем  знак  δφ(t) и Δω_н существенной роли не играет):

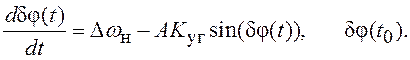                    (7.1)

          Нелинейное дифференциальное уравнение (7.1) удобно решать графическим способом (рис. 7.2). Стрелками показано направление изменения ошибки δφ(t) (при 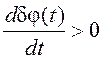 ошибка δφ(t) увеличивается, при  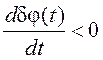- уменьшается). Прямоугольниками обозначены точки устойчивого равновесия исследуемой динамической системы, являющиеся решением уравнения (7.1) (из-за периодического характера дискриминационной характеристики решения уравнения (7.1) неоднозначно).

          В случае нулевой начальной расстройки по частоте (Δω_н=0, рис. 7.2, а) динамическая составляющая ошибки системы ФАПЧ равна нулю: δφ(t→∞)=0. В случае не нулевой начальной расстройки частот (рис. 5.2, б) установившееся значение ошибки отлично от нуля и определяется в результате решения уравнения  Заметим, что для линейной статической характеристики  имеем

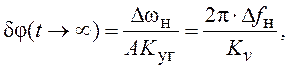                                   (7.2)

 где Δf_н  - начальная расстройка по частоте в Гц; K_v=AK_уг – общий коэффициент усиления линейной системы ФАПЧ, имеющий размерность в∙град/с/в=с^-1 (в разд. 1.7 отмечалось, что фаза формально является безразмерной величиной). Величина 2π∙Δf_н  представляет собой скорость изменения разности фаз φ_с-φ_г, поэтому выражение (7.2) хорошо согласуется с результатами разд. 3.

          Существует такое значение Δω_н= Δω_у=AK_уг, при котором нет точек устойчивого равновесия системы (рис. 7.2, в) и, соответственно, отсутствует конечное значение δφ(t→∞). При этом величина Δf_у=Δω_у/2π называется полосой удержания нелинейной системы ФАПЧ. Значение Δω_у зависит от величины максимального напряжения A на выходе фазового дискриминатора и коэффициента усиления управляемого генератора K_уг: Δf_у=AK_уг /2π.

Таким образом, если расстройка частот входного и опорного напряжений достигнет значения Δf_у, то произойдет срыв слежения. В отличие от режима слежения, когда установившееся напряжение u_фд на выходе фазового дискриминатора постоянно, в режиме срыва слежения u_фд не постоянно и представляет собой биения характерной формы (рис. 7.3). Несимметричная форма биений, при незначительном превышении Δω_н над Δω_у, объясняется действием управляемого

генератора: при u_фд>0 частота опорного напряжения приближается к частоте входного напряжения, а при u_фд<0 – удаляется. Если Δω_н>>Δω_у, быстродействие управляемого генератора оказывается недостаточным для отработки u_фд и форма u_фд приближается к синусоидальной.

          Биения на выходе фазового дискриминатора нелинейной системы ФАПЧ также существуют в режиме захвата (начальная стадия работы системы). Если Δω_н<Δω_у, то наличие постоянной составляющей в напряжении u_фд несимметричной формы приводит к подстройке частоты управляемого генератора с полной компенсацией Δω_н , частота биений уменьшается до нуля и наступает режим слежения. Если Δω_н≥Δω_у, то постоянной составляющей в напряжении u_фд недостаточнол для полной компенсации Δω_н и в системе наблюдается устойчивый режим биений.