Анализ нелинейных систем. Метод гармонической линеаризации. Применение теории марковских процессов для анализа нелинейных систем, страница 11

          Данный результат справедлив, если флюктуационная характеристика дискриминатора не зависит от рассогласования x ( срыв слежения рассматривается, как правило, при наличии интенсивной помехи и это условие выполняется). Кроме того, существенным является допущение о малой вероятности срыва слежения.

Замечание. Оценка вероятности срыва слежения при линейной (в пределах апертуры) дискриминационной характеристике может быть выполнена также с помощью теории выбросов случайных процессов (под выбросом здесь понимается выход ошибки слежения x(t) за границы апертуры дискриминационной характеристики [γ₁, γ₂]). Известно, что распределение выбросов случайного процесса подчиняется закону Пуассона:

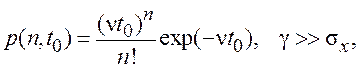                              (7.39)

где p(n,t₀) – вероятность появления за время t₀ ровно n выбросов; ν – средняя частота выбросов (среднее число пересечений процессом x(t) граничного уровня γ в одном направлении в единицу времени); σ_x – среднеквадратическое значение случайного процесса x(t); условие γ>>σ_x соответствует малой вероятности срыва слежения.

          Вероятность появления хотя бы одного выброса за время t₀ определяется, в соответствии с (7.39), соотношением:

                             (7.40)

          При наличии 2-х границ вместо (7.40) следует использовать соотношение:

где ν₁ и ν₂ – средние частоты пересечения уровней γ₁=γ-m_x и γ₂=γ+m_x.

                                                                                            Таблица 7.1.

          Средняя частота пересечения уровня γ относительно просто рассчитывается для линейной (в пределах апертуры [-γ, γ]) дискриминационной характеристики с известной крутизной S:

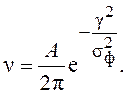                                                  (7.41)

В таблице 7.1 приведены формулы, позволяющие рассчитать параметр A для нелинейных систем с заданной ПФ линейной части W_л(p). Дисперсия флюктуационной составляющей ошибки  определяется известным для линейных систем способом (см. разд. 3).

7.8. Применение теории марковских процесссов для оптимизации нелинейных систем

          Одной из задач, решаемой с использованием устройств радиоавтоматики, является оценивание параметров радиосигнала (амплитуды, частоты, фазы, времени запаздывания и др.). Принимаемый радиосигнал связан почти со всеми перечисленными параметрами (кроме амплитуды) нелинейной зависимостью. Поэтому модель входного воздействия (см. разд. 1.10) включает в себя нелинейное уравнение наблюдения:

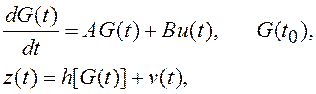                                     (7.42)

где G(t) – вектор состояния формирующего фильтра, описывающего поведение всех оцениваемых параметров (информационных и неинформационных) радиосигнала; h[G(t)] – нелинейное преобразование , зависящее от закона модуляции радиосигнала; u(t) и v(t) - независимые белые шумы с известными СПМ:  и, соответственно, .

          Для построения оценки вектора G(t) необходимо определить условное распределение G(t) при наблюдении z(t):  т.е. апостериорное распределение G(t) (в качестве оценки Y(t) обычно выбирают среднее значение апостериорного распределения, либо такое значение, при котором  максимально).

          Плотность вероятности  и динамика ее изменения во времени описывается дифференциальным уравнением в частных производных, полученным Р.Л. Стратоновичем (1960 г.):

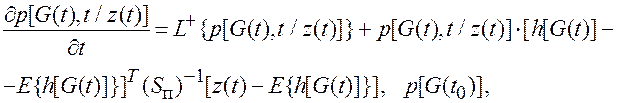     (7.43)

где  - математическое ожидание нелинейного преобразования  относительно апостериорного распределения:   (интегрирование выполняется по всем компонентам вектора G в области его определения); оператор  определен уравнением (7.26).

          Уравнение (7.43) отличается от уравнения Фоккера-Планка-Колмогорова наличием в правой части оператора сжатия , что объясняется накоплением сведений о процессе G(t) при наблюдении z(t).