u=x1(x2+x1+4)+x2(x2+x1+4)+4; p1=1, p2=2; R=3. Спрос и λ - ?
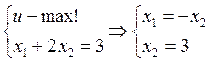
Спрос: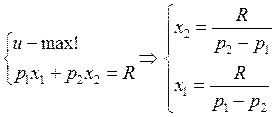 
- спрос на второе и первое благо,
соответсвенно.
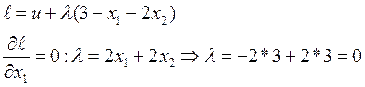
Задача 8
Общий случай: u=x1+v(x2).
v`x2>0;
v``x2<0 à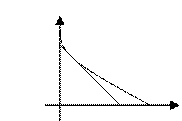 
Граничное решение в двух случаях – либо v(x) – линейная = ax. Либо u – выпуклая функция:
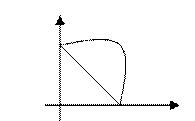MRS = γ12=-u2/u1=-v`x2/1=-v`x2;
v`x2=p2/p1
Задача 9
Опечатка в учебнике: предельная полезность денег равна 3/p1 или в целевой функции поставить вместо 3 – единицу.
u=3x1+√x2
L(λ,x1,x2)=3x1+√x2+λ(R-p1x1-p2x2)à λ=3/p1и x2=p12/4p22
Задача 10
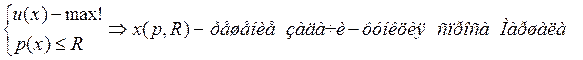Теперь – ν(p,R)=u(x(p,R)) – значение
целевой функции задачи при ценах p и доходе R в точке оптимума.
Можно записать взаимную задачу:
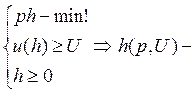
сопоставляет заданному уровню полезности U и ценам p потребительский набор, который обеспечивает наименьший уровень расходов.
e(p,U)=p*h(p,U), где e – функция расходов – значение целевой функции взаимной задачи в точке оптимума при данных ценах и уровне благосостояния. Теорем ВЗАИМНОСТИ!
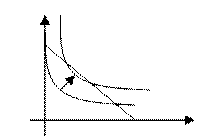
В первой задаче потребитель выбирает максимальный уровень полезности при заданном бюджетном ограничении, в взаимной задаче при заданном уровне полезности потребитель выбирает доход.
Рассмотрим для степенной функции:
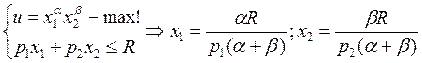
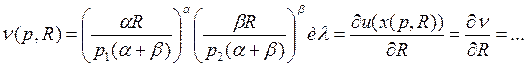
Для функции u=axα1+bxβ2
Для этой функции нужно рассмотреть несколько случаев для различных α и β.
1) α=β=1 à линейная.
2) α,β≥1 и один из них > 1. Функция, очевидно, выпуклая, поэтому решения – на осях. Пусть x2=0.
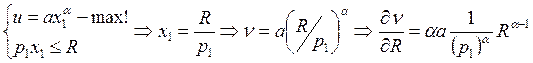
Аналогично, -
оптимум на x2 получаем -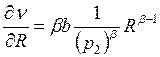 
3) α,β≤1 и один из них < 1.
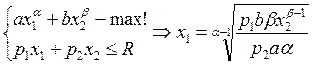. Далее решать стоит, только при заданных
параметрах. J
Для функции u=(x1+a)α+(x2+b)β
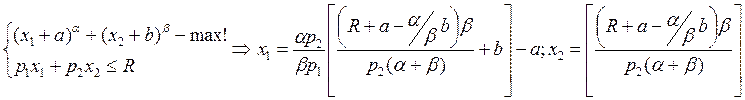
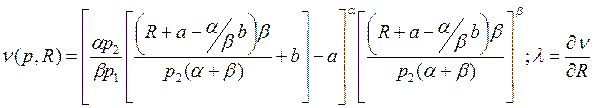
Задача 11
u(x)=ν(p,R) – косвенная функция полезности, x=x(p,R).
ν(p,e(p,U))=u(x)à∂ν/∂pi=[∂ν(p,e(p,U))/∂R]*[∂e(p,U)/∂pi]=0 {ВНИМАНИЕ: e(p,u)=R в точке оптимума}
По лемме Шепарда hi(p,U)=0
U=ν(p,R) (1)
h(p,ν(p,R))=x(p,R) (2)
e(p,ν(p,R))=R (3)
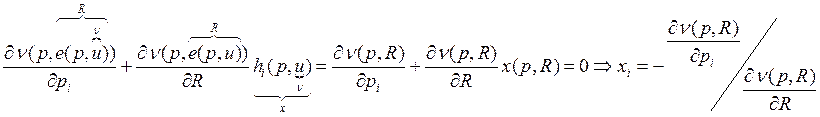
Задача 12
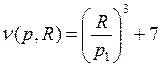
Внимательно посмотрев на предыдущую задачу, замечаем, что для нахождения спроса, необходимо знать производные по pi и R.
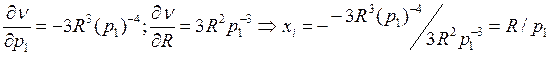
Вид функции – степенная (можно вспомнить, что у неё стоит в числителе – R, а в знаменателе – что-то с ценами)
Задача 13
Вспомним понятие однородности:
Пусть дана функция f(x). Если f(ax)=anf(x), то показатель n – это и есть степень однородности.
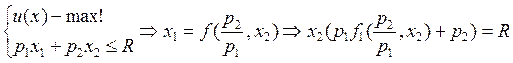
а) x2(αR,p)= x2+αp1/αp2f(αp2/αp1;x2)-αR/αp2=α0x2(R,p)
б) L=u(x1,x2)+λ(R-p1x1-p2x2) à x1=f(p2/p1;x2) и λ=u`x1/p1=g(f(p2/p1;x2);x2)/p1
λ(αX)= g(f(αp2/αp1;x2);x2)/ αp1 = α-1λ(X) ЧТД.
Задача 14
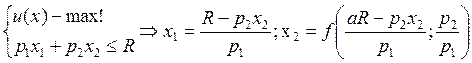
Задача 15
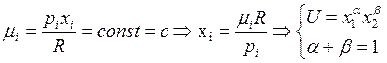
Задача 17
а) e(p,U)=p*h(p,U)
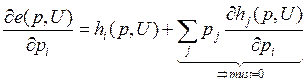
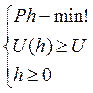По теореме Куна-Таккера существует λ: pj=λ*(∂U/∂hj)
Умножим и
просуммируем на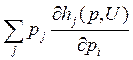
à получим: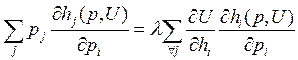 
По определению h: U(h(p,U))=U
Берем производную U по h:
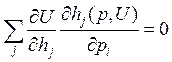ЧТД
б)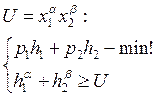 
Нужно выразить H через P и U.
Записываем
Лагранжиан и берем производные по h1 и h2, 
: 
. Получаем:
pj=λ*(∂U/∂hj) à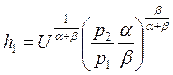 
; 
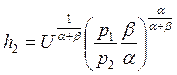
Задача 19
а) v(p,R)=U(x(p,R))
x(p,R)=x(λp, λR)
v(λp, λR)=U(x(λp, λR))=U(x(p,R))=v(p,R)
e(p,U)=λp1h1+...+λpnhn =λe(p,h)
б) h – возрастающая функция от C поэтому e – тоже, так как она получена с помощью монотонного преобразования.
в) ∂e(p,C)/∂pi=hi(p,C)
Задача 21
а) Надо доказать:
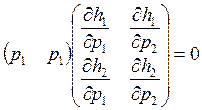
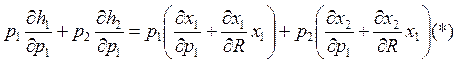
(p1x1+p2x2=R)`Ràp1(∂x1/∂R)=1-p2(∂x2/∂R)
(p1x1+p2x2=R)`p1à p1(∂x1/∂p1)=-x1-p2(∂x2/∂p1)
Подставляем в (*). Получается ,что (*)=0 ЧТД
в) Доказать:
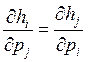
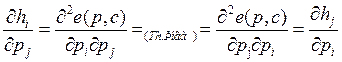
Задача 22
U(x1,x2)= x1+√x2
MUx1/MUx2=2√x2=p1/p2àx2=p12/4p22 и x1=R/p1-p12/4p2
Взаимная задача:
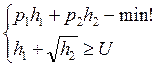Откуда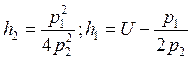 
Тогда уравнение Слуцкого запишется:
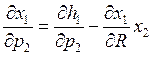и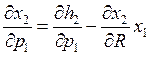 
Осталось
подставить данные J
Задача 23
v(P1,P2,R)=R/min{P1,P2} – косвенная функция полезности. Требуется найти функцию расходов. По условиям теоремы взаимности:
R=e(p,C)
C=v(p,R)
С=e(p,C)/min{P1,P2}àe(p,C)=c*min{P1,P2}
Перемножим e(p,C)*v(P1,P2,R)=1 ЧТД.
Задача 24
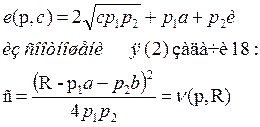
а) Применяем лемму Шепарда:
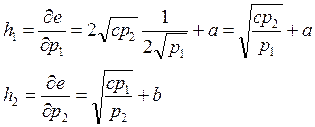
б) Из задачи 11:
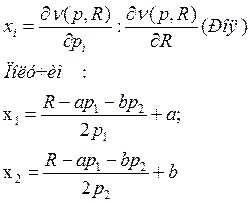
в)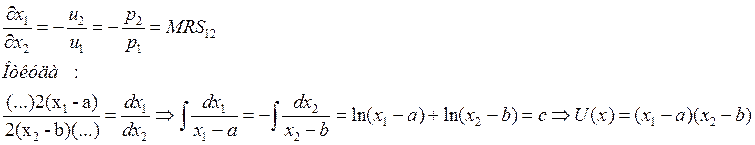 
Задача 25
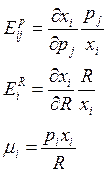Тождество Эйлера: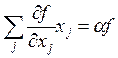 
а)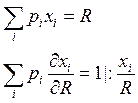 
ЧТД
б) 
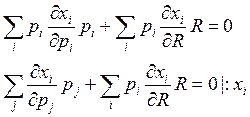
ЧТД
в) 
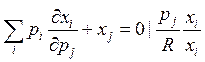
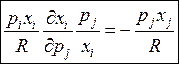
ИЛИ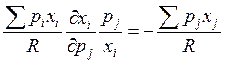 
ЧТД
Задача 26
Задача 27
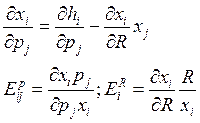
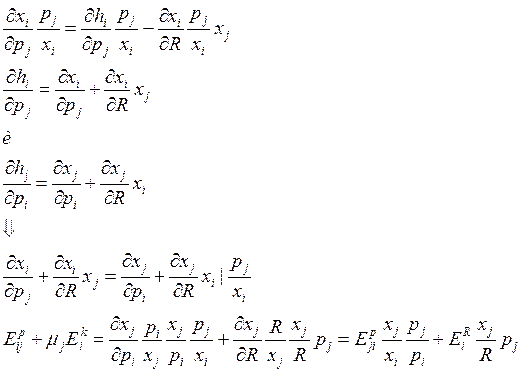
Задача 28
E11=-0.9, E22=-1.5, E1=0.8
а)(1+E11)(1+E22)=E12E21
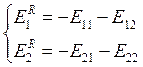àE12=0.1, E21=-0.5, E22=2
μ1*0,8+(1-μ1)*2=1 à μ1=5/6 - бедные
б) E12=0.1, E21=-0.1, E22=1,2
μ1*0,8+(1-μ1)*1.2=1 à μ1=0.5 - средние
Задача 29
U(X)=x1+v(x2)
p1x1+p2x2≤R
∂x2/∂R=0; (∂x2/∂R)*(R/x2)=0; E2R=0; -(E11+E12)=E1R; E21=-E22; μ1E1R=1
Задача 30
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.