Пример выполнения курсовой работы с помощью ЭВМ, страница 5

Тогда

     По данным значениям  и  по круговым диаграммам определяем значкние запаса устойчивости по амплитуде  равное

     Участок средних частот представлен на рисунке 2.7.

 

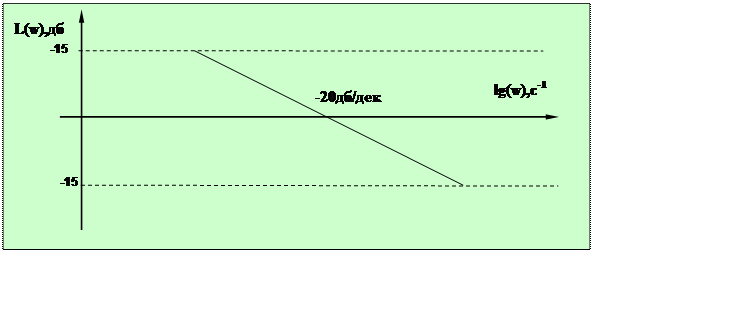Рисунок 2.7- Участок средних частот

     Участок высоких частот не корректируют, он строится параллельно участку высоких частот некорректированной системы. На рисунке 2.8 представлен желаемая логарифмическая амплитудно-частотная характеристика.

 

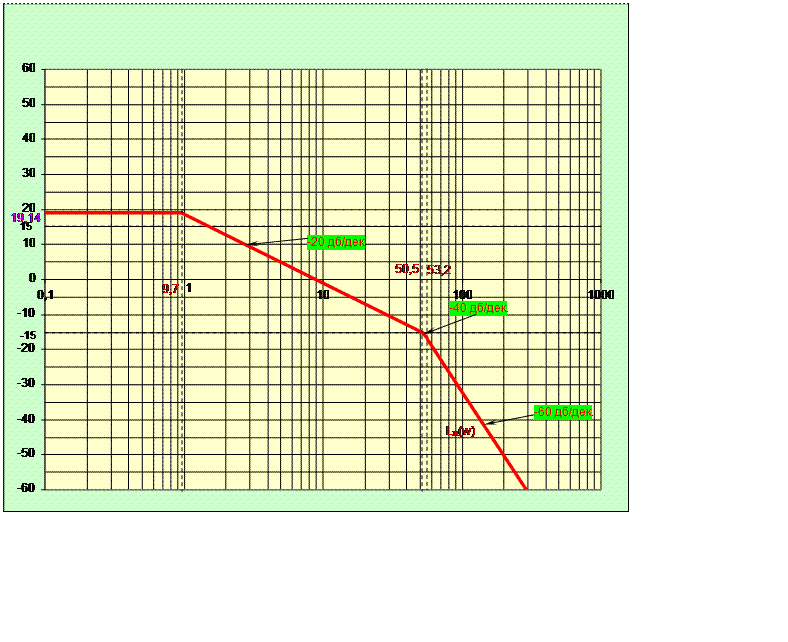Рисунок 2.7- Желаемая логарифмическая амплитудно-частотная характеристика

«Оглавление»

2.4* Нахождение корректирующего устройства

     В курсовой работе выбрано последовательное корректирующее устройство, так как оно требует меньших затрат сил и времени при расчете и проще включается в цепь.

     Логарифмическая амплитудно-частотная характеристика корректирующего устройства находится графическим вычислением.

      Результат приведен на рисунке 2.9

 

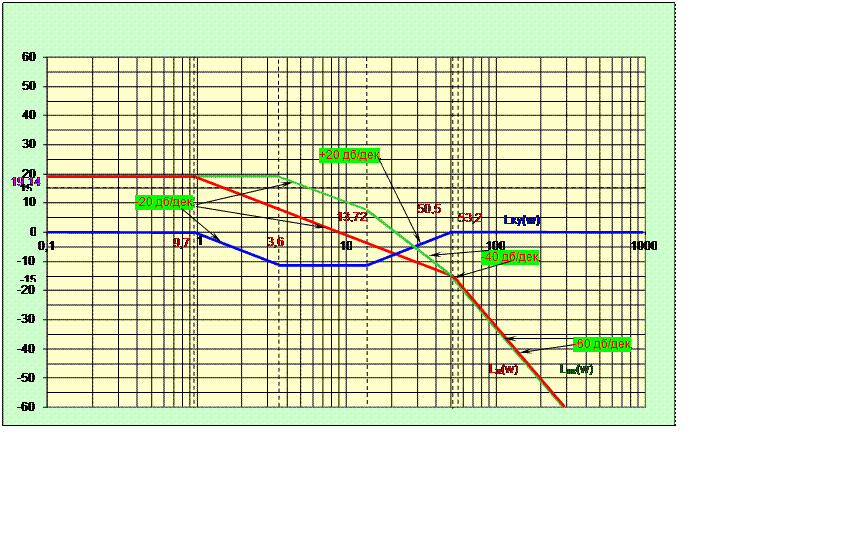
Рисунок 2.9- Нахождение логарифмической амплитудно-частотной характеристики корректирующего устройства

     Полученную характеристику можно реализовать одной элементом с логарифмической амплитудно-частотной характеристикой изображенной на рисунке 2.10. Из справочника [3[БММ15] ] выбрана цепочка с такой характеристикой (рисунок 2.11)

 

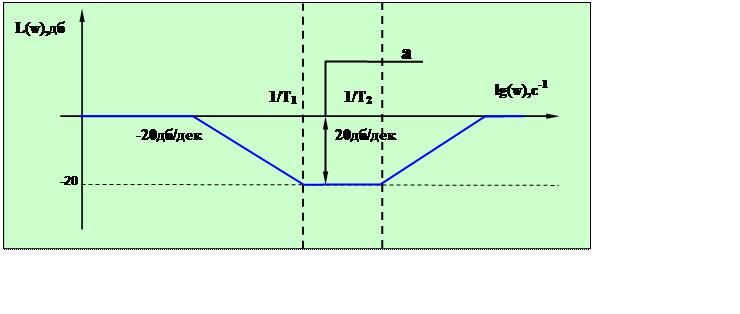Рисунок 2.10- Логарифмическая амплитудно-частотная характеристика корректирующего устройства

.

 

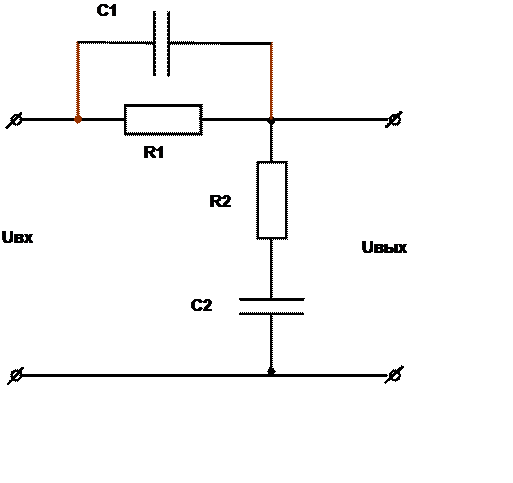Рисунок 2.11- Схема корректирующего пассивного контура

Передаточная функция этой -цепочки имеет вид:

,

,

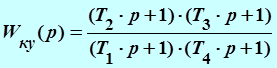тогда

.

где   ,

         .

        

        

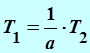
      Из рисунка 2.10 следует, что

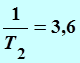, (сек^-1),

тогда

 (сек),

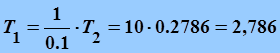 (сек);

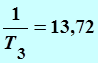,(сек^-1),

тогда

 (сек);

 (сек);

Для расчета значений элементов схемы сперва зададимся :

  (кОм)      

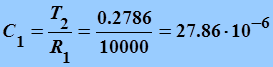 (мкФ);

Значение элемента схемы вычислим  по следующему выражению:

,

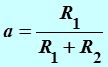следовательно

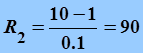  (кОм),

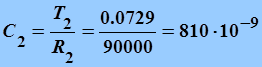 (нкФ);

По стандартному ряду:

  (Ом),

 (мкФ),

  (Ом),

 (нкФ),

Тогда передаточная функция этой -цепочки будет иметь вид:

,

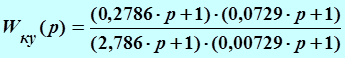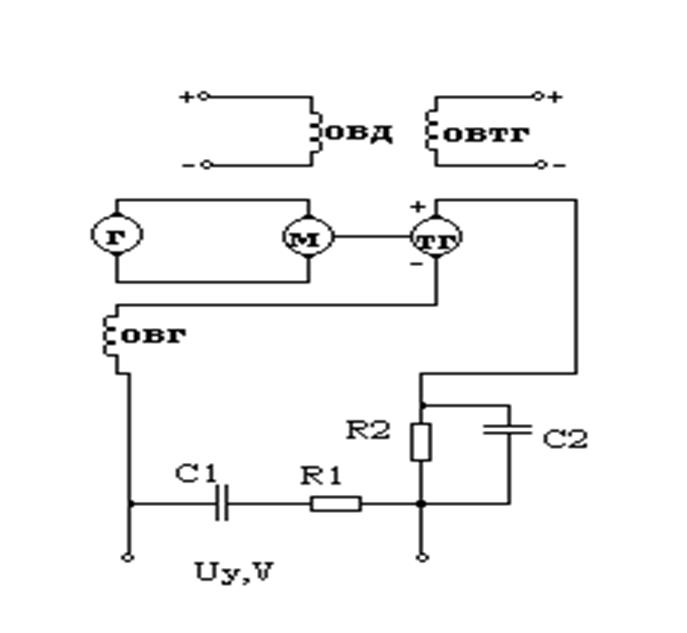
Рисунок 2.12 - Схема включения КУ в АСР

«Оглавление»

2.5* Нахождение скорректированной передаточных функций разомкнутой и замкнутой системы

      Так как рассчитанное нами корректирующее устройство последовательное  то  разомкнутую передаточную функцию системы найдем путём  перемножения не корректированной системы с корректирующим устройством.

Тогда разомкнутую передаточную функцию системы будет иметь вид:

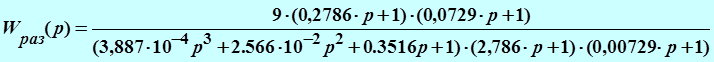
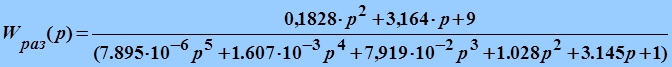
     а замкнутая  передаточная функция системы:

«Оглавление»

2.6*  Проверка на устойчивость скорректированной АСР

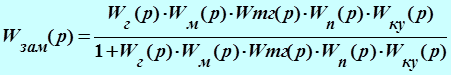
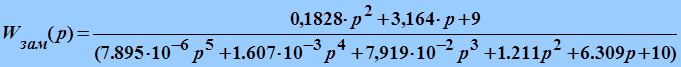
Передаточная функция скорректированной разомкнутой АСР имеет вид:

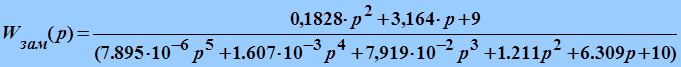
Исследуем устойчивость системы с помощью частотного критерия Михайлова. Для этого выделим характеристическое уравнение замкнутой системы, сделаем замену p = jw:, построим годограф Михайлова. Так как система третьего порядка, то для того чтобы система была устойчива нужно чтобы годограф начинался на вещественной положительной оси и проходил последовательно три квадранта при изменении  от 0 до .Это можно пронаблюдать на рисунке 2.14 и 2.15 на котором представлен годограф Михайлова.

Данные для построения годографа Михайлова приведены в таблице 2.1.

Таблица 2.1 -  Данные для построения годографа Михайлова

	0	1	5	7	8,5	10	15	20
	10	8,8	-19,271	-45,48	-69,11	-95,03	-181,121	-217,28
	0	6,23	21,671	17,134	5,34	-15,311	-166,636	-482,076

Продолжение  таблицы 2.1 -  Данные для построения годографа Михайлова