Аналитическая геометрия на плоскости и в пространстве, страница 12

Пример 1. Составить канонические и параметрические уравнения прямой, проходящей через точку Р₁(2, -3, 4) параллельно прямой   .

Решение. Так как направляющий вектор а(3, 5, -2) данной прямой является направляющим вектором искомой прямой, то канонические уравнения искомой прямой таковы:   . Параметрические уравнения имеют вид

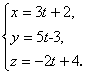
Пример 2. Составить канонические и общие уравнения прямой, проходящей через точку

А(3, -5, 1) параллельно оси Oz.

Решение. Направляющий вектор прямой а равен орту k оси Oz: a = k = (0, 0, 1), поэтому канонические уравнения прямой имеют вид . Запишем два уравнения

. Тогда общие уравнения прямой имеют вид

Пример 3. В плоскости Oyz найти прямую, проходящую через точку Р₁(0, 2, -5) перпендикулярную прямой .

Решение. Так как прямая принадлежит плоскости Oyz, то направляющий вектор прямой  и . Находим 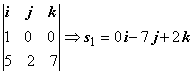. Канонические уравнения прямой, проходящей через точку Р₁(0, 2, -5):           .

Пример 4. Составить канонические и параметрические уравнения прямой, проходящей через точки Р₁(4, 3, -1) и Р₂(2, -3, 6).

Решение. В качестве направляющего векторы возьмем Р₁Р₂ = (-2, -6, 7), поэтому канонические уравнения прямой имеют вид  . Параметрические уравнения: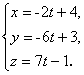  

Пример 5. Привести к каноническому виду общие уравнения прямой .

Решение. Запишем векторы нормалей к данным плоскостям: n₁(3, 2, -1), n₂(1, -4, 2). Находим направляющий вектор прямой: s = n₁xn₂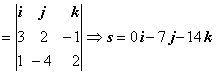. За направляющий вектор прямой можно взять вектор, коллинеарный найденному: s(0, 1, 2). Найдём точку, принадлежащую прямой, положив y = 0. Решая систему 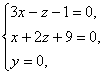, находим точку Р₁(-1, 0, -4). Kанонические уравнения прямой            .

Пример 6. Найти косинус угла между прямыми  и

Решение. Направляющий вектор первой прямой a₁(2, 1, 3). Векторы нормалей к плоскостям

N₁(5, 3, -1) и N₂(2, 1, 2). Найдём направляющий вектор второй прямой: 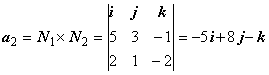. Косинус угла между прямыми .

Пример 7. Проверить, скрещиваются ли данные прямые  и  и найти расстояние между ними.

Решение. Нам известны направляющие векторы a₁(4, -3, 5) и a₂(1, 0, 2) данных прямых и точки Р₁(-3, 0, 2), Р₂(0, -1, 4), принадлежащие этим прямым, тогда вектор . Проверим выполнение условия некомпланарности: 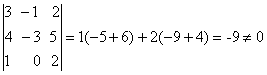, следовательно, данные прямые скрещиваются.