Применение уравнения Эйлера для решения задач теории оптимального управления. Безградиентные методы. Оптимизация функции одной переменной, страница 3

Далее рассматривается отрезок [0; Х₂] внутри этого отрезка относительно центра находят новые точки Х₃ и Х₄ , которые располагаются симметрично относительно центра на величину ε/2.

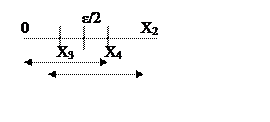
Находят значения G в т. Х₃ и Х₄ , сравнивают полученные значения. Предположим интервал неопределенности смещен вправо , в результате ранее рассмотренный отрезок с корд. [Х₃; Х₂].

Внутри этого отрезка находят новую пару значений Х₅ и Х₆ и т. д.

Процесс продолжается до тех пор, пока длина оставшегося интервала неопределенности не примет значения:

N – количество заданных шагов поиска extr.

Особенностью метода является то, что эффективность очередной пары значений снижается по сравнению с эффективностью предыдущей пары.

Как, было отмечено (перед пр-ром) особенностью рассмотренной схемы расчетов является то, что эффективность расчета пары экспериментов снижается по сравнению эффективности предыдущей пары, например – если к некоторому моменту окажутся израсходованными η пар, где η<N/2, то величина интервала неопределенности для израсходованных η-пар составит: ,

Если выполнить следующий шаг и использовать еще одну пару, то длина неопределенности составит:

В результате интервал уменьшится на Δ:

Делаем вывод: Выигрыш Δ  тем меньше, чем больше η. В пределе если η→∞, Δ→0.

На практике целесообразно использовать 7-8 пар, хотя теоретически возможность расположения новой пары точек внутри интервала неопределенности точек сохраняется.

Для выбора величины ε, можно использовать физ. соображения, например – при расчете оптимального режима какого-либо объекта нет смысла использовать extr. значения переменных с большей точностью, чем они могут поддерживаться соответствующими приборами и устройствами.

Следовательно величина ε м. б. выбрана в соответствии со статической погрешностью схемы.

4.1)Сис-му ограничений записывают в виде равенств: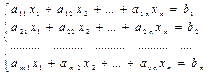

х_j≥0, j=1,2…n.

Целевую ф-ю F приводят к виду F→min.

2)Выбирают m – базисных переменных и выбирают их через (n-m) свободных переменных, в результате получают 1-й базис, в котором матрица коэф-в, при базисных переменных будет единичной, на этом шаге получают первое базис-е реш-е.

3)Среди коэф-в при свободных переменных целевой ф-и  есть хотя бы один отрицательный (С_j<0), следовательно, можно улучшить решение. Если таких отрицательных оценок несколько, то выбирают наибольшую по модулю, тогда столбец с индексом j будет разрешающим (ведущим).

4)Выбирают ведущую строку из условия min-го отношения  

Коэф-т вычисляют только для тех строк для которых коэф-ты а_ij  полож-ны. Если коэф-т а_ij<0, то для него не вычисляется.

5)Каж. элемент ведущей строки делят на разрешающий элемент добиваясь, чтобы коэф-т при переменной х_j был = 1, в рез-те образ-ся новая строка Симплекс-таблицы, котрая записывается на прежнее место в новой таблице.

6)В остальных строках Симплекс-таблицы исключают переменную х_j, добиваясь, чтобы во всех строках коэф-ты при этих переменных были =0. В рез-те переменная  х_j входит в базис, а некоторая переменная х_i выходит из базиса.

7)Опр-т новое базисное реш-е и новое значение F. Вычисляют вектор относительных оценок, (-строку), путем элементарных преобразований, либо при помощи правила скалярного произведения.

8)Проверяют полученное решение на оптимальности. Если реш-е не яв-ся оптимальным, т.е. в -строке есть отриц-е относительные оценки, то повторяют алгоритм с п.3.

5.Оптимизация функции одной переменной.

Для поиска опт-го значения ф-и исп-т классические методы анализа, в основе которых лежит дифференц. исчесление ф-и одной  переменной.

Ф-я у=f(x) имеет локальный min (локальный max) в точке х₀, если сущ-т нек. положит-я величина δ, при которой выпускается неравенство: /х-х₀/<δ, а также выполняется условие f(x)≥f(x₀)- для задач минимизации; f(x)≤ f(x₀)-для задач максимизации.

Ф-я у=f(x) имеет глобальный min в точке х^* если для всех х выполняется условие f(x)≥f(x^*), где f(x^*) –точка глобального max.

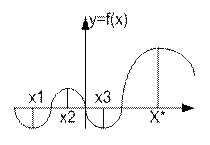
х3-точка глобального min; х1- глобальный min; х2-глобальный max; х*- глобальный max

Необходимое условие существования локального экстремума ф-и: должна быть равна нулю производная первого порядка.

Достаточное условие существования локального экстремума ф-и: смена знака производной при переходе через точку экстркмума.

Если производная меняет знак с полож-го на отриц-ный, то в рассматриваемой точке х₀ находится max, если знак производной меняется с отриц-го на полож-ный, то в точке х₀ ф-я достигает min.