Применение уравнения Эйлера для решения задач теории оптимального управления. Безградиентные методы. Оптимизация функции одной переменной, страница 2

Предположим значения функции G(x) на концах исходного интервала [a,b]известны, а также значения функции известны в некоторых внутренних точках исходного интервала [a,b] и в т. Х₁ и Х₂. Т. к. значения функции G(x) известно в этих точках, то можно выбрать один из 2-х подинтервалов [Х₀; Х₂] или [Х₁; Х₃]. В одном из этих интервалов локализуется extr. функции G(x).

Отношением: , называется золотым сечением, которое обладает следующей особенностью: если в исходном интервале [Х₀; Х₃] внутренние точки Х₁ и Х₂ отстоят от концов интервала на величину z, в любом из образующихся подинтевалов можно так выбрать положение новой точки Х₄ , которая будет отстоять от концов своего подинтервала на величину z.

Т. о. при использовании метода золотого сечения имеется возможность с помощью одного вычисления на каждом этапе локализировать положение extr. внутри интервала, длина которого составляет 1-z=0.62 от длины исходного интервала.

Алгоритм поиска extr.:

1). Вычисляем значения функции G(x) на концах исходного интервала [a,b] т. е. значения G(Х₀) и G(Х₃).

2). Вычисляем значения функции в точке Х₁ = Х₀ +0,38(Х₃ - Х₀ )

3). Вычисляем значения функции в точке Х₂ = Х₃ -0,38(Х₃ - Х₀ )

4). Сравнивают полученные значения  G(Х₁) и G(Х₂) и по результатам сравнения выбирают подинтервал в котором локализуется extr.

Эти новые 2-а подинтервала состоят из 2-х участков l1 и l2.

5). Внутри большого отрезка (l₁) находится точка отстоящая от концов отрезка (l₁+l₂) на величину 0,38. В этой точке рассчитывается значения функции G(x) и вновь определяют подинтервал внутри интервала (l₁+l₂) и т. д.

Точность метода золотого сечения оценивается по формуле, учитывающей границы отрезка , где a, b – границы интервала, на котором определяется extr. функции S – число вычислений функции G(x).

Методы с использованием чисел Фибоначчи.

Свойство чисел Фибоначчи можно использовать для поиска extr. функции одной переменной G(x). Свойство последовательности чисел Фибоначчи описывается рекуррентным соотношением F_к = F_k-1 + F_k-2 , где F₀ = F₁ =1.

Ряд значений чисел Фибоначчи приведен в таблице

Алгоритм поиска min с использованием метода Фибоначчи (min):

1). По заданной точности ε находят количество шагов, т. е. вспомогательное число N, где , где a,b – границы рассматриваемого интервала внутри которого разыскивается положение функции G(x).

2). Для полученного значения N находят такое число для которого бы выполнялось условие (пользуясь таблицей) F_s-1 <N< F_s .

3). Определяется min-й шаг поиска extr. по найденному числу

4). Рассматривается значения функции G(x) В начале интервала [a,b], т. е. рассчитывается значение G(а).

5). Определяется следующая точка из [a,b] в которой рассчитывается значение функции G(x) по выражению: .

6). Рассчитывается значение функции G(x) в этой найденной новой точке G().

Выполняют сравнение полученных значений G(x) и G(). Если шаг оказался удачным G()<G(x), то определяется новая точка [a,b] по выражению: .

7). Выполняют расчет в новый точке G() и т. д. до тех пор пока шаг окажется неудачным.

В случае неудачного шага расчет новой точки выполняется по выражению например, для

8). Последующие шаги алгоритма выполняются с уменьшающейся величиной шага, которую определяют по выражению: , где i=0, 1, 2,…- номер шага.

В результате этого алгоритма используется вся последовательность чисел Фибоначчи в убывающем порядке.

Метод дихотомии.

Дихотомия – половина деления. Идея метода: из N – экспериментов находят интересующий интервал [Х₁; Х₂], Х₁ и Х₂ – это два значения отрезка, которые рассматриваются как единичный отрезок. Значения Х₁ и Х₂ рассматриваются внутри исходного интервала N – экспериментов наилучшим образом, в смысле определенного критерия качества G(x), т. е. эти значения располагаются симметрично относительно центра исходного интервала на расстоянии ε/2 (ε – заданная точность)

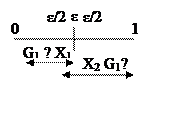
В т. Х₁ и Х₂ вычисляется значения цел. функции, и их сравнивают, сравнивая полученные значения, можно определить гарантируемый интервал неопределенности G₁=(1±ε)/2.

Предположим этот интервал неопределенности смещен влево. В результате получаем интервал отрезка между точками [0; Х₂].