3) в следующей 2–й строке все элементы вновь делим на новое значение а’22 и затем повторяем п. 2 для этих i–х строк, вычитая уже 2–ю строку и т.д.
Пример
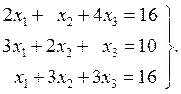
Отсюда расширенная матрица [A, b]
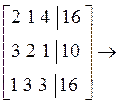
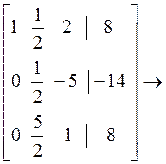
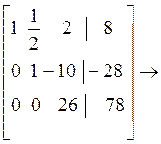
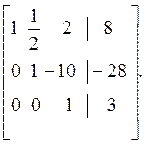
И окончательно получаем
Или в обычном виде
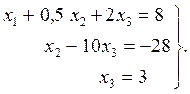
Разновидностью метода исключения является алгоритм Гаусса–Жордана, в котором матрица [A] преобразуется в единичную, а [b] – в столбец с искомыми неизвестными х1 , х2, …, хm , т.е. [A, b] преобразуется в [I, x].
Для этого операцию по п. 2 алгоритма Гаусса надо применить и к выше лежащим строкам.
Рассмотрим тот же пример
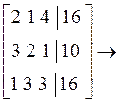
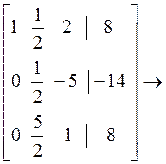
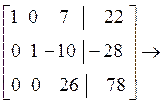
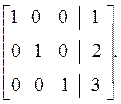
Или в обычном виде

LU-разложение
Все виды гауссова исключения связаны с разложением неособенной квадратной матрицы А в произведение двух треугольных – нижней L и верхней U, т.е. А = LU. Это позволяет представить систему Ах = b в виде LUх = b, которая сводится к системам
Ly = b; Uх = y.
Из–за треугольности L и U уравнения решаются без обращения матриц.
Матрица L, как и матрица U, формируется в ходе гауссова исключения, но ее k–й столбец состоит из элементов k–го столбца матрицы А, полученных на предыдущем (k – 1)–м шаге. Т.е. нужно на каждом шаге по главной диагонали и ниже ее сохранять предыдущие значения элементов.
В результате получают квадратную матрицу LU, при чем на диагонали U берутся единицы, а не ее значения.
Тот же пример:
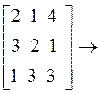
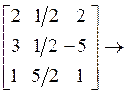
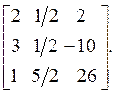
Откуда матрицы L и U равны
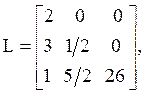
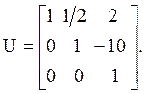
Определитель |А| равен произведению диагональных элементов матрицы L
![]()
Наконец получаем две системы уравнений:
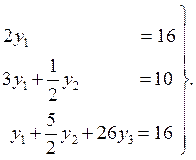
Это уравнение вида Ly = b.
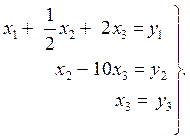
Это уравнение вида Ux = y.
Дифференциальные уравнения
ДУ 1–го порядка
![]()
имеет решение
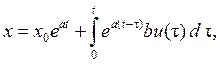
где х0 – начальное значение при t = 0; a и b – постоянные коэффициенты. Для матричного уравнения
![]()
решение таково
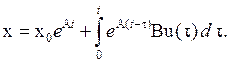
Для нормальной однородной системы ДУ
![]()
решение имеет вид
![]()
Подставим х в исходное уравнение
![]()
![]()
Последнее уравнение имеет решение, если
![]()
или
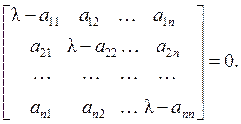
![]() – это многочлен n–й степени, т.е.
– это многочлен n–й степени, т.е.
![]()
Корни уравнения дают значения l i , при которых система ДУ имеет решения.
При простых (попарно различных) корнях уравнения D(l) = 0 и l = l i из однородного уравнения (l i I – A) h( i ) = 0 можно найти вектор h ( i ) . Решение системы ДУ для корней l i будет x( i ) = h( i ) e l i t. Всего таких уравнений будет n.
Для матрицы А матрица |l I – A| называется характеристической, D(l) = 0 – характеристическим уравнением, его корни l i – собственными значениями, а h( i ) – собственными векторами матрицы А.
Общее решение системы имеет вид:
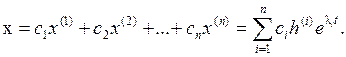
Считая х (i) столбцами матрицы Х, а ci – элементами столбца произвольных постоянных с , запишем:
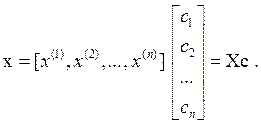
В свою очередь
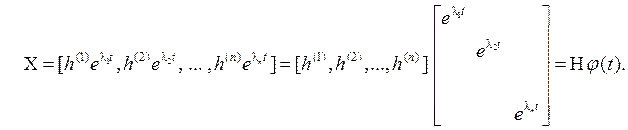
В итоге решение однородной системы
![]()
При t = 0 матрица j (t) = I, а х0 = Н с. Откуда с = Н –1 х0, а общее решение
х = Н j (t) Н –1 х0 = Ф(t) х0 ,
где Н – модальная матрица,
Ф(t) – фундаментальная матрица.
Для ее определения необходимо знать собственные значения и собственные векторы матрицы А системы ДУ.
Для примера рассмотрим однородную систему ДУ
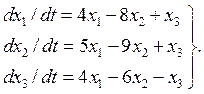
Для нее
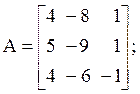
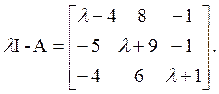
Характеристический многочлен D (l) получим разложением по 1–й строке. Алгебраические дополнения таковы:
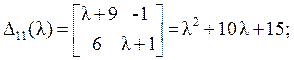
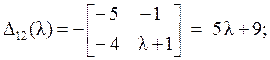
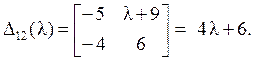
Отсюда D (l) и собственные значения равны:
![]()
Собственные векторы находятся из выражения:
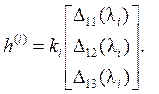
Или
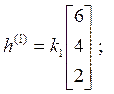
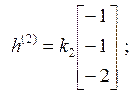
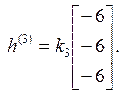
Значения коэффициентов ki произвольны, берутся из соображений удобства. Примем k1 = 1/2, k2 = –1, k3 = 1/6. Тогда модальная матрица и обратная к ней
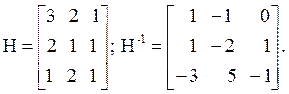
Фундаментальная матрица
Ф(t)
х = Н j (t)
Н –1 =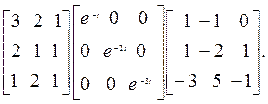
Так как х = Ф(t) х0 , то с учетом начальных условий x10 , x20 , x30
x1 = (3e –t + e –2t – 3e –3t ) x10 + (–3e –t – 2e –2t + 5e –3t ) x20 + (e –2t – e –3t ) x30;
x2 = (2e –t + e –2t – 3e –3t ) x10 + (–2e –t – 2e –2t + 5e –3t ) x20 + (e –2t – e –3t ) x30;
x3 = (e –t + 2e –2t – 3e –3t ) x10 + (–e –t – 4e –2t + 5 e –3t ) x20 + (2e –2t – e –3t ) x30.
Экспонента от матрицы
Матрицу j(t) можно записать
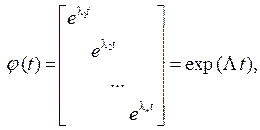 где
где 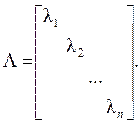
Подставляя Ф(t) = Н j (t) Н –1 в уравнение входа dx(t)/dt = Ax(t), получим
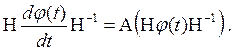
Умножая слева на Н–1 и справа на Н, получим
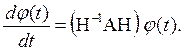
Отсюда важные соотношения
L = Н–1А Н , а А = Н L Н–1.
Таким образом, любую квадратную матрицу А с различными собственными значениями можно преобразовать в диагональную матрицу, элементы которой – эти собственные значения.
Поэтому экспоненциальную функцию от матрицы А находят по формуле
exp (At) = H exp (L t) H–1.
Тогда Н будет матрицей преобразования переменных ДУ, т.е. х = Н у.
Подставим х в исходное уравнение
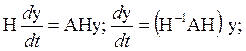
![]()
То есть замена переменных приводит к ДУ с диагональной матрицей, а исходная система уравнений «развязывается» относительно новых переменных. Или
![]()
![]()
Для неоднородной системы ДУ
![]()
решение имеет вид
![]() (1)
(1)
Подставим х(t) в исходное уравнение
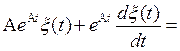
![]()
После упрощений
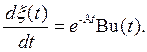 (2)
(2)
Начальное значение ![]()
Интегрированием (2) получаем
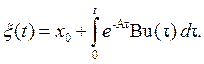 (3)
(3)
Подставляя (3) в (1), найдем решение неоднородной системы ДУ
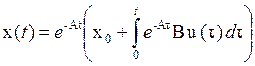
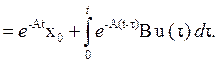
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.