Матрицы
Это совокупность элементов, расположенных в виде таблицы. В обозначении элементов аi j i – номер строки, j – номер столбца матрицы. В зависимости от типа элементов матрицы бывают вещественными и комплексными. Если А комплексная матрица с элементами аi j = a i j + jb i j , то матрица с элементами а*i j = a i j – jb i j называется комплексно – сопряженной.
Если число строк и столбцов равны, то матрица квадратная. Если в ней всего одна строка или один столбец, то матрицу называют вектором – строкой или вектором – столбцом.
Совокупность ii–клеток называют главной диагональю квадратной матрицы. Если все остальные элементы равны нулю, то матрицу называют диагональной, записывая кратко
А = diag(а1, а1, … , аn).
Диагональная матрица
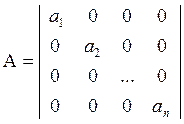
Если все элементы диагональной матрицы равны 1, то она единичная матрица I (или Е) n–го порядка. Если все элементы матрицы (n x m) равны нулю, то она нулевая, обозначается 0.
Квадратная матрица называется верхней U (нижней L) треугольной, если равны нулю все элементы, расположенные под (над) главной диагональю.
Единичная матрица
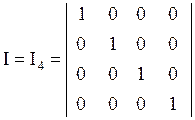
Верхняя треугольная матрица
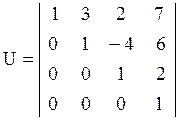
Нижняя треугольная матрица
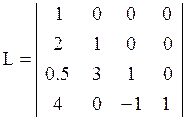
Сумма матриц А и В одинакового размера – это матрица С того же размера, каждый элемент которой ci j равен сумме соответствующих элементов матриц А и В: аi j + bi j.
Произведение матрицы А (m x n) на В (n x r) – это матрица С (m x r), элемент которой ci j равен сумме произведений элементов i–й строки А на элементы j–го столбца В.
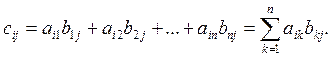
Умножение А на В допустимо, т.е. произведение существует (матрицы согласуются по форме), если число столбцов А равно числу строк В.
Различают умножение матриц слева и справа, ибо их результаты не одинаковы.
При замене строк матрицы А на столбцы получают транспонированную матрицу Ат.
Если матрица А совпадает со своей транспонированной, т.е. А = Ат , то она называется симметричной (относительно главной диагонали). Если А = – Ат , то матрица называется кососимметричной (диагональные элементы равны нулю).
Симметричная матрица
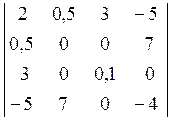
Кососимметричная матрица
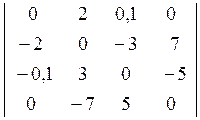
Комплексно–сопряженная и транспонированная матрица называется сопряженной с А и обозначается А*.
Если матрица А = А*, то она называется эрмитовой; если А = –А*, то она называется косоэрмитовой матрицей.
С матрицами можно производить обычные вычислительные действия – возводить в степень, дифференцировать, интегрировать.
Эрмитова матрица
Матричное уравнение Ах = q решается умножением обеих частей слева на обратную матрицу А–1, т.е.
А–1 Ах = А–1 q или х = А–1 q .
По правилу Крамера неизвестные хk
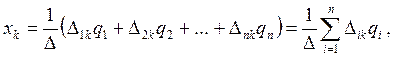
где D – определитель матрицы, det A;
D ik – алгебраические дополнения, которые вычисляются как определитель матрицы, полученной вычеркиванием из матрицы А i–й строки и k–го столбца, умноженный на (–1) i + k .
Часто определитель обозначают |А| , алгебраическое дополнение Аik . Обратную матрицу находят, умножив присоединеннную матрицу adj А на D–1.
Обратная матрица существует, если det A¹ 0 , т.е. матрица А неособенная (невырожденная). (АВ)–1 = А–1 В–1 .
Для упрощения вычислений матрицы можно разбить на блоки. Такие блочные матрицы допускают обычные действия над собой. Это уменьшает размеры вычисляемых матриц и очень удобно, если можно выделить нулевые блоки.
Блочная матрица
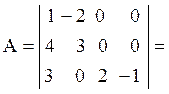
Если в определителе n–го порядка выделить k различных строк и столько же различных столбцов, то их элементы образуют свой определитель – минор k–го порядка Мk . Оставшиеся элементы других (n – k) строк и столбцов образуют дополнительный к Мk минор (n – k) –го порядка .
Миноры из строк и столбцов с одинаковыми номерами i i называют главными (диаг. элементы D).
Определитель D n–го порядка выражается через элементы аi j любой его строки или столбца и алгебраические дополнения D i j этих элементов как
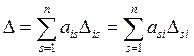
![]()
Это позволяет представить определитель n–го порядка через определители (n – 1)–го порядка.
Наиболее просто вычисляется определитель треугольной или диагональной матрицы: он равен произведению диагональных элементов.
Линейные уравнения
Для решения системы неоднородных уравнений Ax = b используют метод исключения неизвестных в алгоритме Гаусса. Для этого берут расширенную матрицу системы [А, b] и за счет операций над ее строками преобразуют в матрицу [U, y] , где U – верхняя треугольная матрица с единицами на главной диагонали, y – преобразованный столбец свободных членов. И вместо A x = b:
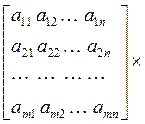
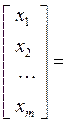
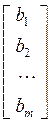
получим уравнение U x = y, или
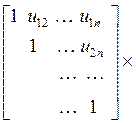
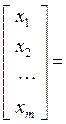
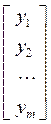
из которого легко последовательно найти неизвестные хm, хm–1, …, х1.
Для такого преобразования (Гаусса):
1) в первой строке [A, b] все элементы делим на первый элемент а11;
2) прибавляем к каждой i–й строке первую строку, умноженную на – аi 1 , получая первый столбец с единственным ненулевым элементом 1;
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.