Поведение ![]() -
функции показано на рисунке 5.7.
-
функции показано на рисунке 5.7. ![]() - функция не
падает скачком до нуля при
- функция не
падает скачком до нуля при ![]() как это было в
случае ящика с бесконечно высокими стенками.
как это было в
случае ящика с бесконечно высокими стенками.
Это означает, что существует вероятность для частицы выйти
из ямы, когда ее энергия Е меньше глубины ямы ![]() .
Решение задачи о частице в потенциальной яме имеет практические значения.
Короткодействующие ядерные силы, действующие между электроном и протоном, можно
представить в виде прямоугольной потенциальной ямы и найти энергию
связи.
.
Решение задачи о частице в потенциальной яме имеет практические значения.
Короткодействующие ядерные силы, действующие между электроном и протоном, можно
представить в виде прямоугольной потенциальной ямы и найти энергию
связи.
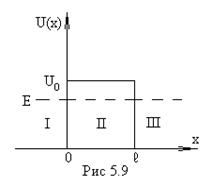 Рассмотрим
частицу, которая движется слева на право, встречая на своем пути потенциальный
барьер высоты
Рассмотрим
частицу, которая движется слева на право, встречая на своем пути потенциальный
барьер высоты ![]() и ширины
и ширины ![]() (рис.5.9). По
классическим представлениям поведение частицы имеет следующий характер. Если
энергия частицы больше высоты барьера (
(рис.5.9). По
классическим представлениям поведение частицы имеет следующий характер. Если
энергия частицы больше высоты барьера (![]() )
то частица беспрепятственно проходит над барьером, на участке (
)
то частица беспрепятственно проходит над барьером, на участке (![]() ) лишь уменьшается скорость частицы,
но затем при
) лишь уменьшается скорость частицы,
но затем при ![]() она снова
принимает первоначальное значение.
она снова
принимает первоначальное значение.
Если же Е меньше ![]() ,
то частица отражается от барьера и летит обратно, сквозь барьер она проникнуть
не может.
,
то частица отражается от барьера и летит обратно, сквозь барьер она проникнуть
не может.
Согласно же квантовой теории даже при ![]() имеется отличная от нуля вероятность
того, что частица проникнет сквозь потенциальный барьер и попадет в область
имеется отличная от нуля вероятность
того, что частица проникнет сквозь потенциальный барьер и попадет в область ![]() . Такое поведение частицы
вытекает из решения уравнения Шредингера.
. Такое поведение частицы
вытекает из решения уравнения Шредингера.
Рассмотрим частицу, подлетающую к барьеру с энергией ![]() . Уравнение Шредингера для такой
частицы имеет вид:
. Уравнение Шредингера для такой
частицы имеет вид:
I. ![]()
![]() ,
,
III. ![]()
![]() ,
,
II. ![]()
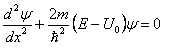
( то же, что и для ящика с конечными стенками, только Е без модуля).
При этом разность ![]() . Волна
де Бройля, соответствующая частице, частично отражается от стенок барьера,
частично проходит сквозь них, поэтому решения уравнения Шредингера для
выделенных на рис. 5.9 областей принимают вид:
. Волна
де Бройля, соответствующая частице, частично отражается от стенок барьера,
частично проходит сквозь них, поэтому решения уравнения Шредингера для
выделенных на рис. 5.9 областей принимают вид:
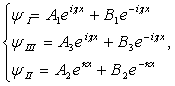 (5.5)
(5.5)
где 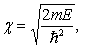
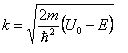 ,
, ![]() -
амплитуда прямой волны,
-
амплитуда прямой волны, ![]() - отраженной,
- отраженной, ![]() .
.
В области III имеется только волна, распространяющаяся слева направо:
![]() ,
,![]() ,т.к.
,т.к.
![]() соответствует волне, распространяющейся
справа налево.
соответствует волне, распространяющейся
справа налево.
Запишем граничные условия. В силу непрерывности ![]() - функции имеем:
- функции имеем:
![]() .
(5.6)
.
(5.6)
Для того чтобы ![]() - функция была
гладкой (не имела изломов) необходимо, чтобы ее первая производная была
непрерывной
- функция была
гладкой (не имела изломов) необходимо, чтобы ее первая производная была
непрерывной
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.