Лекция 8
5. СТАЦИОНАРНЫЕ ЗАДАЧИ КВАНТОВОЙ МЕХАНИКИ
5.1.Частица в потенциальном ящике с бесконечно высокими стенками
Рассмотрим частицу, находящуюся в бесконечно
глубокой одномерной потенциальной яме. Будем считать, что частица может
двигаться только в направлении оси ОХ. Стенки ямы бесконечно высокие и
представляют собой параллельные плоскости (рис.5.1). Такую прямоугольную яму
называем ящиком. Она является упрощенной моделью атома водорода, в котором
движется электрон. 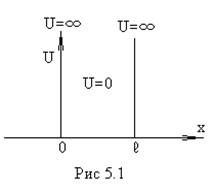 Потенциальная
энергия частицы
Потенциальная
энергия частицы
в ящике равна нулю, а за пределами
ящика ![]() . Уравнение Шредингера
Шредингера
для такой частицы имеет вид:
. Уравнение Шредингера
Шредингера
для такой частицы имеет вид:
![]() .
.
B ящике U=0, поэтому ![]() .
.
Обозначим
![]() .
(5.1)
.
(5.1)
Тогда
![]() .
.
Это известное из теории колебаний уравнение синусоидальной волны, причем k , определяемое уравнением (1) – волновое число. Решение этого уравнения имеет вид:
![]() .
(5.2)
.
(5.2)
При решении уравнения Шредингера должны выполняться граничные условия:
- так как стенки ящика бесконечно высокие, то вероятность
обнаружить частицу за пределами ящика равна нулю ![]() =0.
Однако
=0.
Однако ![]() - непрерывная функция,
следовательно,
- непрерывная функция,
следовательно, ![]() на границах ящика также
должна обращаться в ноль:
на границах ящика также
должна обращаться в ноль: ![]() , тогда
, тогда ![]() и
и ![]() ;
на правой границе ящика
;
на правой границе ящика ![]() ,
поэтому
,
поэтому ![]() n=1,
2…. Отсюда
n=1,
2…. Отсюда
![]() .
(5.3)
.
(5.3)
При n=0
![]() и
и ![]() -
вероятность обнаружить частицу хотя бы в какой-то точке пространства равна
нулю, т.е. частица нигде не находится. Такого быть не может, поэтому значение п=0
лишено физического смысла..
-
вероятность обнаружить частицу хотя бы в какой-то точке пространства равна
нулю, т.е. частица нигде не находится. Такого быть не может, поэтому значение п=0
лишено физического смысла..
Условие (5.3) означает что волновое число k может принимать только некоторые разрешенные значения в зависимости от целого числа п , т.е. квантуется. Из условия (5.3) также следует, что по дну ящика должно укладываться целое число полуволн де Бройля, что совпадает с условием возникновения стоячих волн в струне.
Действительно, подставим ![]() в
уравнение (5.3), имеем:
в
уравнение (5.3), имеем:
![]() ;
и
;
и ![]() .
.
Пусть частица летит к стенке ящика (рис.5.2). Справа от стенки происходит наложение двух волн де Бройля, соответствующих частице – прямой и отраженной, распространяющихся в противоположных направлениях. Стенка абсолютно отражающая, поэтому амплитуда падающей волны равна амплитуде отраженной волны, и в ящике образуется стоячая волна.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.