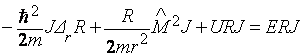 .
.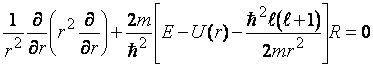 .
.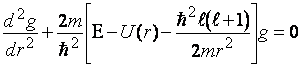 . (7.5)
. (7.5)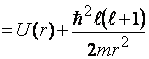 . Дальнейшее решение требует знания
вида потенциала U(r).
. Дальнейшее решение требует знания
вида потенциала U(r).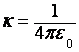 .
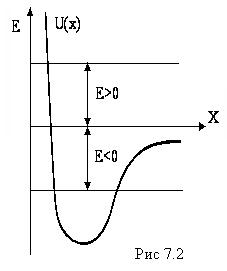
.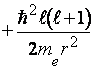 ,
, где
где 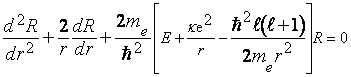 .
.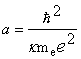 -
постоянная, называемая боровским радиусом (a = 0,52∙
-
постоянная, называемая боровским радиусом (a = 0,52∙Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.