Глава 2. О возможности использования математической модели для целей повышения точности инерциальных систем навигации.
2.1 Общие замечания.
Сущность предлагаемого
метода повышения точности инерциальной навигационной системы
(ИНС),рассматриваемая на примере ИНС полуаналитического (ПА) типа, заключается
в том, что в контур физического построителя вертикали включается математическая
модель построения вертикали. Указанная математическая модель сформирована
таким образом, что после суммирования выходного сигнала физического
(механического) построителя с выходным сигналом математического модельного
построителя вертикали(параметры которого подобранны определенным
образом),достигается высокая (очень высокая) степень компенсации погрешностей
ИНС, зависящих от всех составляющих дрейфа гироскопических чувствительных
элементов. В результате указанной компенсации происходит адекватное повышение
точности ПА ИНС в выработке навигационной информации о курсе объекта α,
приращения составляющих линейной скорости объекта (![]() и
и ![]() ), а так же приращению широты и долготы
местоположения объекта (
), а так же приращению широты и долготы
местоположения объекта (![]() и λ ). Следует особо
отметить, что нижеследующие математические операции имеют в виду морские
объекты, движущиеся сравнительно медленно по отношению к линейно скорости точки
Земли, расположенной на экваторе.
и λ ). Следует особо
отметить, что нижеследующие математические операции имеют в виду морские
объекты, движущиеся сравнительно медленно по отношению к линейно скорости точки
Земли, расположенной на экваторе.
В качестве отправных математических основ теории ПА ИНС используются работы {1},{2}, а так же первоначальная (в принципиальном плане), но недостаточно эффективная ) с точки зрения повышения точности ИНС ) математическая модель впервые предложенная в монографии автора {3}.
Необходимо особо подчеркнуть, что в результате проделанного исследования удалось практически полностью исключить ошибку ПА ИНС за счет неизбежного существования дрейфа у гироскопических чувствительных элементов что, впрочем, считалось наиболее трудно решаемой и наиболее актуальной проблемой.
2.2 Отправные математические основы теории ПА ИНС.
Указанные отправные математические основы изложены в [1].
Кинематические уравнения ошибок в определении навигационной информации на выходе ПА ИНС имеют следующий вид:
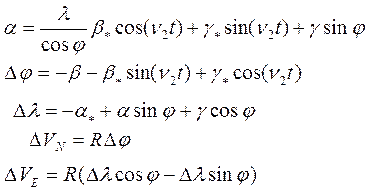
![]()
Уравнения ошибок аналитического
аналога инерциального построителя координат (для случая ![]() ,
,
![]() ,
,![]() )
)
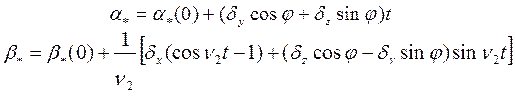
![]()
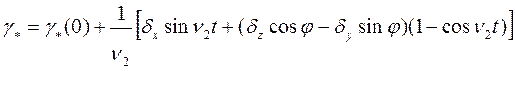
 |
Дифференциальные уравнения ошибок механического аналога (гиростабилизированной платформы) горизонтной системы координат в моделировании вертикали объекта
![]()
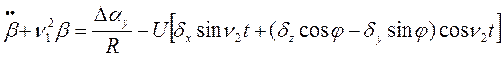
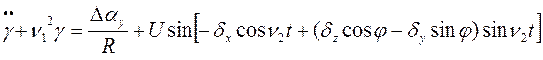
Общие решения дифференциальных уравнений ошибок механического аналога {3}
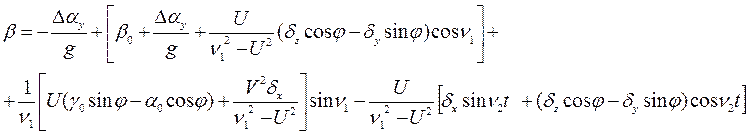
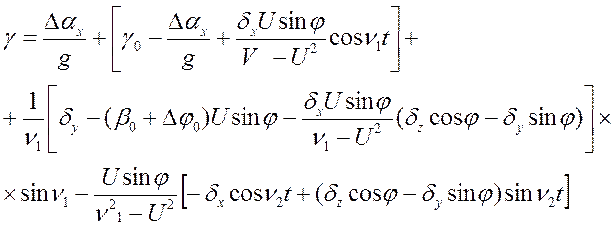
Общие решения для кинематических уравнений ошибок в определении навигационной информации на выходе ПА ИНС (т.е. уравнений (1))
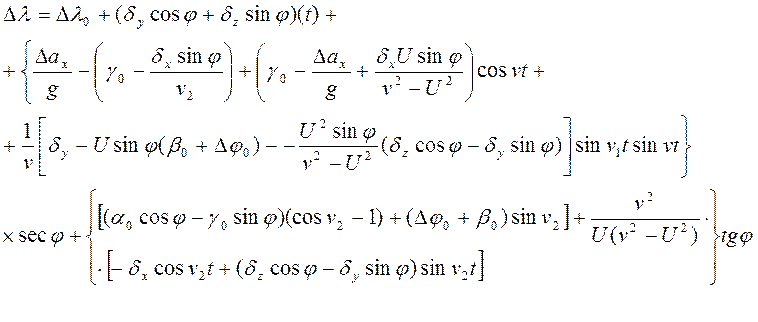
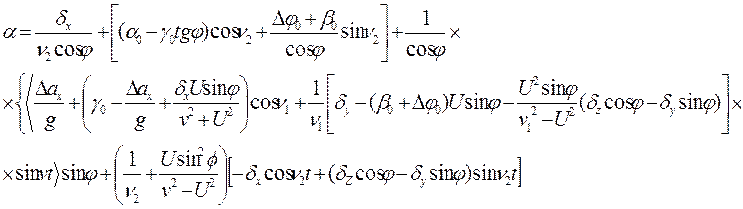
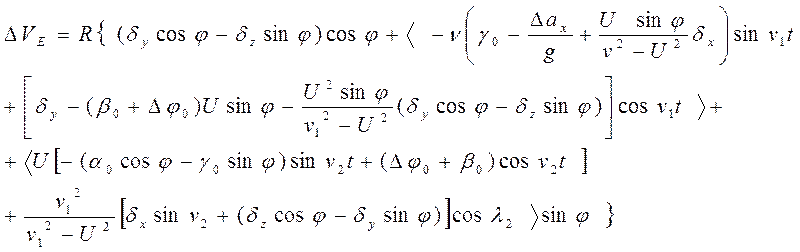
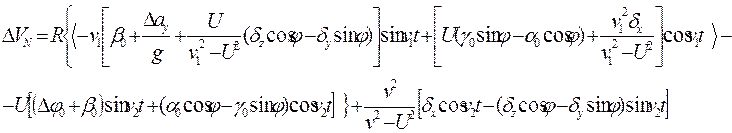
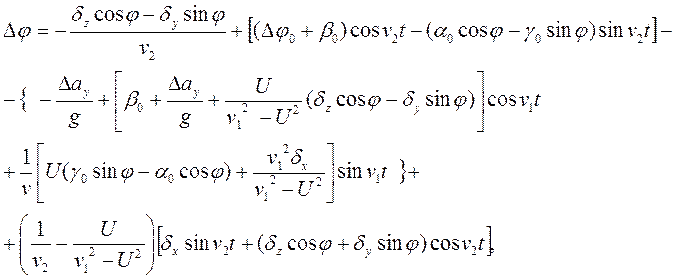
![]()
Сводка условных обозначений, используемая в выражениях (1),(2),(3),(4),(5):
α - азимутальная ошибка механического аналога (гиростабилизированной платформы);
![]() ,
,![]() - ошибки (координаты отклонения от истинных
величин) механического аналога (гиростабилизированного платформа) в моделировании
вертикали объекта;
- ошибки (координаты отклонения от истинных
величин) механического аналога (гиростабилизированного платформа) в моделировании
вертикали объекта;
![]() ,
,![]() ,
,![]() - ошибка в измерении
линейных ускорений объекта;
- ошибка в измерении
линейных ускорений объекта;
![]() ,
,![]() ,
,![]() - ошибка аналитического
аналога (в вычислительном устройстве) инерциальной системы координат;
- ошибка аналитического
аналога (в вычислительном устройстве) инерциальной системы координат;
![]() (0),
(0),![]() (0),
(0),![]() (0) -
ошибки начальных значений;
(0) -
ошибки начальных значений;
![]() -
приращение широта и долгота объекта;
-
приращение широта и долгота объекта;
V, ΔVN, ΔVE, - приращение составляющих от истинных величин;
U - угловая скорость суточного вращения Земли; t - время;
![]() ,
,![]() - широта и долгота объекта;
- широта и долгота объекта;
R - радиус Земли;
![]() ,
,![]() ,
,![]() - угловая скорость
дрейфа гироскопов;
- угловая скорость
дрейфа гироскопов;
![]() = (Ut+
= (Ut+![]() )=(Ut+
)=(Ut+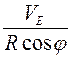 t)=(U+
t)=(U+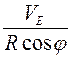 )t=υ2t;
)t=υ2t;
![]() = (U+
= (U+![]() )=U+
)=U+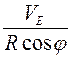 = υ2;
= υ2;
Δay, Δax, - ошибки значений в измерении линейных ускорений объекта.
Для дальнейших операций целесообразны решения (4) записать в более компактной форме, а именно:
![]()
![]() 1t+Csin
1t+Csin![]() 1t+Dsin
1t+Dsin![]() 2t+Ecos
2t+Ecos![]() 2t;
2t;
где
A= –![]() , B=
, B= ![]() +
+![]() +
+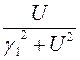 (
(![]() cos
cos![]() sin
sin![]() ),
),
C= ![]() [U(
[U(![]() sin
sin![]() cos
cos![]() )+
)+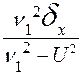 ], D= –
], D= –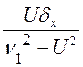 ,
,
![]() Е= –
Е= – 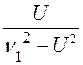 (
(![]() cos
cos![]() sin
sin![]() ).
).
![]()
![]() t+ Lsin
t+ Lsin![]() t+ Mcos
t+ Mcos![]() t+ Nsin
t+ Nsin![]() t,
t,
![]()
где
F= ![]() , K=
, K=![]() –
–![]() +
+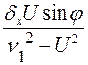 ,
,
L= ![]() [
[![]()
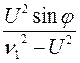 (
(![]() cos
cos![]() sin
sin![]() )],
)],
M=
–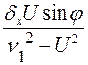 , N=
, N=![]()
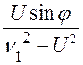 (
(![]() cos
cos![]() sin
sin![]() ).
).
2.3. Общие соображения о структуре математической модели.
Представляется естественным и логичным использовать в качестве математической модели дифференциального уравнения (3,а) следующее неоднородное дифференциальное уравнение второго порядка:
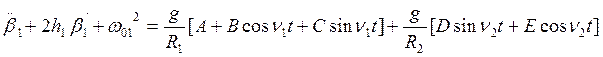 , (10)
, (10)
и, соответственно, для дифференциального уравнения (3,б) следующее неоднородное дифференциальное уравнение также второго порядка:
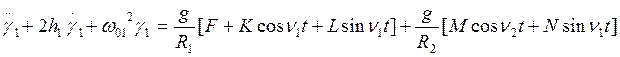 ,
(11)
,
(11)
Из уравнений (10) и (11) вытекает, что внешнее возмущающее воздействие указанных уравнений формируется на основе выходных сигналов соответствие северного и восточного акселерометров, представленных в цифровой форме.
Коэффициенты пропорциональности
взяты в виде: ![]() (для возмущающего воздействия с
частотой
(для возмущающего воздействия с
частотой ![]() ) и
) и ![]() (для
возмущающего воздействия с частотой
(для
возмущающего воздействия с частотой ![]() ).
).
Следует отметить, что частоте ![]() соответствует период М.Шулера Т
соответствует период М.Шулера Т![]() и частоте
и частоте ![]() суточный
период Т
суточный
период Т![]() .
.
Конкретные значения
коэффициентов h![]() ,
,![]() ,R
,R![]() и R
и R![]() определяются ниже.
определяются ниже.
Основная цель использования
математических моделей заключаются в том, чтобы при суммировании цифровых
сигналов, соответственно ![]() и
и ![]() , а также
, а также ![]() и
и ![]() обеспечить минимизацию значений тех ошибок
(в кинематических уравнениях, определяющих навигационную информацию ПА ИНС (см.
формулы(4)),которые возникают в следствие существования дрейфов гироскопов
стабилизированной платформы.
обеспечить минимизацию значений тех ошибок
(в кинематических уравнениях, определяющих навигационную информацию ПА ИНС (см.
формулы(4)),которые возникают в следствие существования дрейфов гироскопов
стабилизированной платформы.
Обратимся вновь к уравнению (10).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.