Составление математической модели задачи. Решение задачи линейного программирования графическим методом. Решение задачи симплекс-методом и с исполь­зованием компьютера (пакет Ехсеl), страница 8

Так как минимальное число линий (5) соответствует порядку матрицы, можно искать оптимальное решение «по нулям» матрицы.

Находим в матрице С строку или столбец с единственным нулем. Это третий столбец. В них единственный ноль . Подчеркнем его, вычеркнув при этом все нули в третьей строке. Получаем матрицу:

.

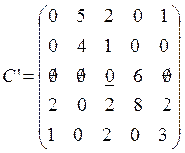Это означает, что в оптимальном решении . Следовательно, никакая площадка, кроме третьей не может принять третий вид продукции, т.е. . Но, согласно условию задачи ни первый, ни второй, ни четвертый, ни пятый вид продукции не может быть принят на третьей площадке, т.е. . Получим:

.

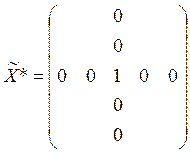В матрице C’ среди неотмеченных нулей находим строку или столбец с единственным нулем. Этому условию удовлетворяет ноль в четвертом столбце. Тогда в матрице  элемент , а . Получаем:

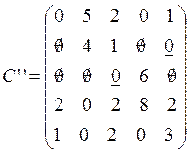, а     .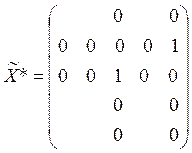

Это означает, что вторая продукция – фиктивна.

В матрице  среди невыделенных нулей единственный ноль находится в первом столбце. Подчеркнем его. При этом вычеркнем все нули в первой строке. По аналогии в матрице  элемент , а . Получаем:

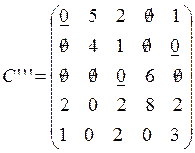, а    .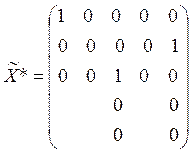

В матрице  среди невыделенных нулей единственный ноль находится в первом столбце. Подчеркнем его. При этом вычеркнем все нули в четвертом столбце. По аналогии в матрице  элемент , а  и . Получаем:

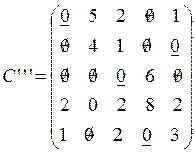, а    .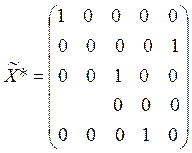

Подчеркиваем последний невыделенный ноль (), единственный в четвертой строке и получаем:

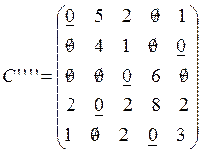, а .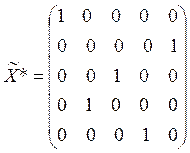

Так как последний столбец фиктивный, то отбросив его, получим оптимальный план исходной задачи:

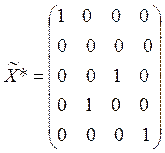, а .

Интерпретация задачи: при максимизации целевой функции в оптимальном варианте второй вид продукции следует исключить. Первый вид принять на первой площадке, третий вид – на третьей площадке, четвертый вид – на второй площадке, а пятый вид – на четвертой площадке. При этом затраты составят 19 единиц.

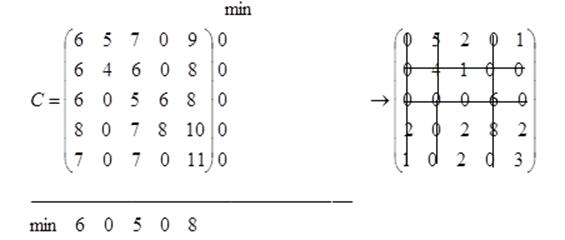
б) задача минимизируется.

Для решения задачи минимизации целевой функции необходимо перейти к закрытой модели, т.е. к исходной матрице С добавить нулевой столбец (как в задаче 3б(а)):

Получим матрицу пятого порядка (n = 5).

Из каждой строки матрицы С вычтем ее минимальный элемент.

.

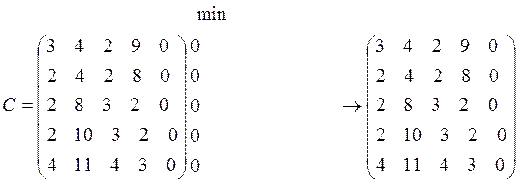Из каждого столбца полученной матрицы вычтем его минимальный элемент.

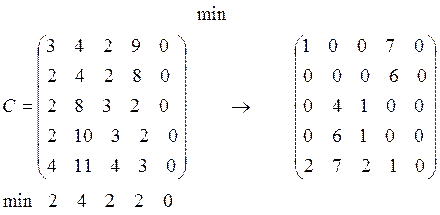
В полученной матрице наименьшим числом горизонтальных и вертикальных линий вычеркнем все нули матрицы.

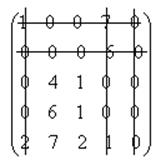
Так как число лини равно 5 и n =  5, оптимальное решение находим «по нулям».

В последней матрице найдем строку или столбец, где находится единственный нуль. Это пятая строка. Возьмем пятую строку, в ней единственный нуль . Подчеркнем его. Это означает, что продукция 5-го вида должна быть доставлена на 5-ю торговую площадку.

.

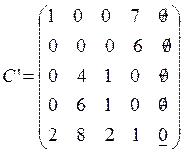Соответственно в матрице X*, являющейся оптимальным решением задачи, элемент , а элементы

. Получаем:

.

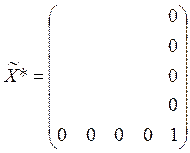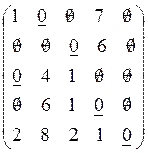
Оставшиеся нули могут быть подчеркнуты разными способами:

Либо так:

, что соответствует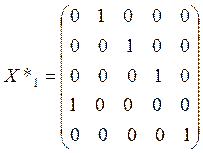   

Либо так:

, что соответствует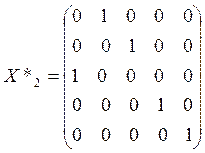   

Получили два возможных решения задачи. Так как затраты по обоим вариантам одинаковы (), то предприятие может выбрать любо из них.

Так как последний столбец фиктивный, то отбросив его, получим оптимальный план исходной задачи:

Или

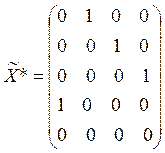, а         .

Или

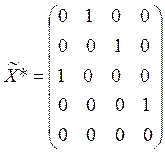, а         .

Интерпретация задачи: при минимизации целевой функции в оптимальном варианте пятый вид продукции следует исключить. Первый вид принять на второй площадке, второй вид – на третьей площадке, третий вид – на четвертой площадке, а четвертый вид – на третьей площадке. Или первый вид принять на второй площадке, второй вид – на третьей площадке, третий вид – на первой площадке, а четвертый вид – на четвертой площадке.

При этом затраты составят 10 единиц.

Спивсок литературы

1.  Бородич С.А. Эконометрика. – Минск: Новое Знание, 2001.

2.  Экономико-математические методы: Методические указания и задания / Под ред. Н.В. Шаланова. – Новосибирск: СибУПК, 2001. – 40 с.