Решить обе задачи. Сделать интерпретацию полученного оптимального решения.
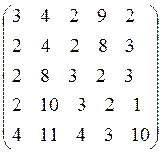
Решение
Задача о назначении является частным случаем транспортной задачи.
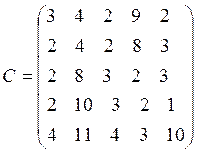
Задача 3а.
Составим математическую модель задачи. Для этой цели введем переменные:
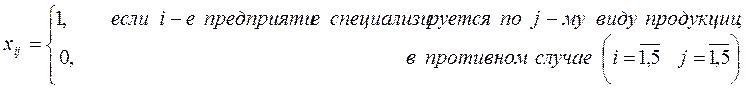 ,
,
тогда матрица:
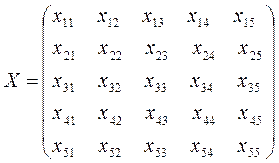 – план распределения.
– план распределения.
Математическая модель задачи о назначении с максимизацией целевой функции будет иметь вид:
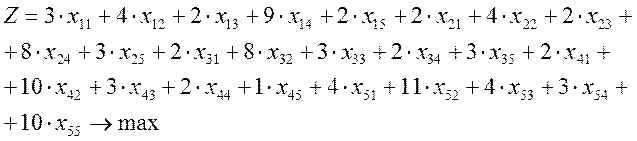
при ограничениях:
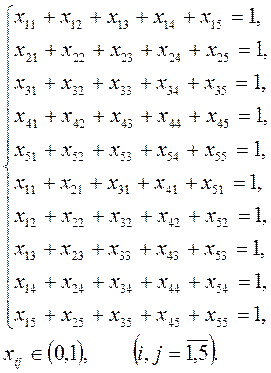
а) задача максимизируется.
Для получения оптимального решения перейдем к задаче о назначении с минимизацией целевой функции:
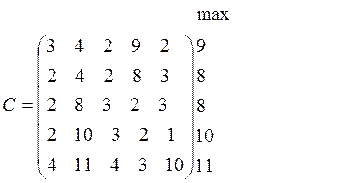
Вычитая элементы строк соответственно из чисел 9, 8, 8, 10, 11, получим матрицу C’. Затем, используя алгоритм о назначении с минимизацией целевой функции получим:
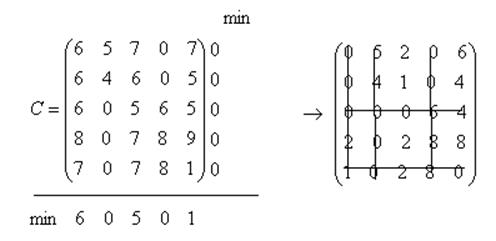
Минимальное число линий равно 5 и равно n (n = 5), «по нулям» находим оптимальное решение.
В последней матрице найдем строку или столбец, где
находится единственный нуль. Это пятый столбец и четвертая строка. Возьмем
четвертую строку, в ней единственный нуль ![]() .
Подчеркнем его. Это означает, что продукция 4-го вида должна быть доставлена на
2-ю торговую площадку.
.
Подчеркнем его. Это означает, что продукция 4-го вида должна быть доставлена на
2-ю торговую площадку.
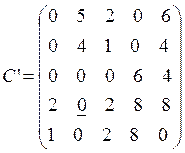
Следовательно, согласно условию задачи на вторую площадку продукция ни первого, ни второго, ни третьего, ни пятого вида поступить не может.
Поэтому во втором столбце вычеркнем все остальные нули.
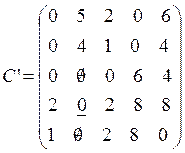 .
.
Соответственно в матрице X*, являющейся
оптимальным решением задачи, элемент ![]() , а элементы
, а элементы ![]()
![]() . Получаем:
. Получаем:
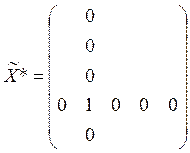 .
.
Оставшиеся нули могут быть подчеркнуты разными способами:
Либо так:
 , что соответствует
, что соответствует 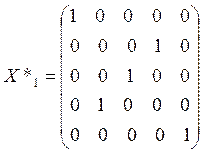
![]() .
.
Либо так:
 , что соответствует
, что соответствует 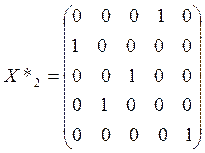
![]() .
.
Получили два возможных решения задачи. Так как затраты
по обоим вариантам одинаковы (![]() ), то предприятие может
выбрать любо из них.
), то предприятие может
выбрать любо из них.
б) задача минимизируется.
Из каждой строки матрицы С вычтем ее минимальный элемент.
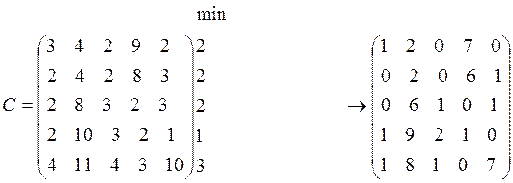 .
.
Из каждого столбца полученной матрицы вычтем его минимальный элемент.
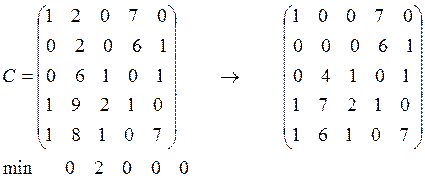
В полученной матрице наименьшим числом горизонтальных и вертикальных линий вычеркнем все нули матрицы.
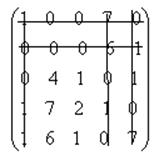
Так как число лини равно 5 и n = 5, оптимальное решение находим «по нулям».
В последней матрице найдем строку или столбец, где
находится единственный нуль. Это четвертая строка, пятая строка и четвертый
столбец. Возьмем четвертую строку, в ней единственный нуль ![]() . Подчеркнем его. Это означает, что
продукция 4-го вида должна быть доставлена на 5-ю торговую площадку.
. Подчеркнем его. Это означает, что
продукция 4-го вида должна быть доставлена на 5-ю торговую площадку.
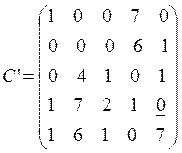 .
.
Следовательно, согласно условию задачи на пятую площадку продукция первого вида поступить не может.
Поэтому во втором столбце вычеркнем все остальные нули.
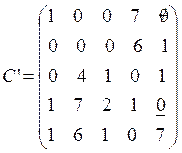 .
.
Соответственно в матрице X*, являющейся
оптимальным решением задачи, элемент ![]() , а элементы
, а элементы ![]()
![]() . Получаем:
. Получаем:
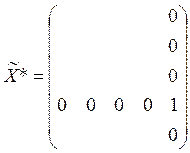 .
.
Оставшиеся нули могут быть подчеркнуты разными способами:
Либо так:
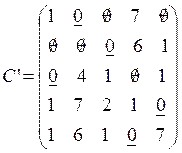 что соответствует
что соответствует 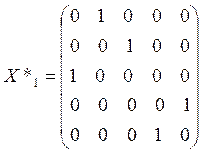
![]() .
.
Либо так:
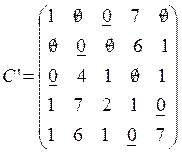 что соответствует
что соответствует 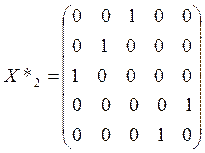
![]() .
.
Получили два возможных решения задачи. Так как затраты
по обоим вариантам одинаковы (![]() ), то предприятие может
выбрать любо из них.
), то предприятие может
выбрать любо из них.
Задача 3б.
Согласно условию задачу получим матрицу:

Составим математическую модель задачи. Для этой цели введем переменные:
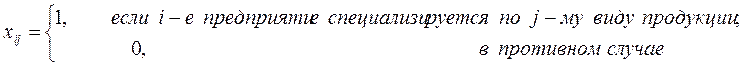 ,
,
тогда матрица:
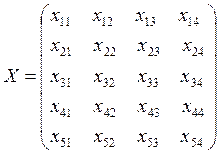 – план распределения.
– план распределения.
Математическая модель задачи о назначении с минимизацией целевой функции будет иметь вид:
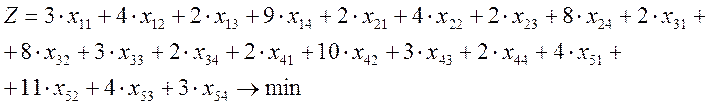
Так как ![]() , одна из строк будет
состоять из нулей. Так как заранее неизвестно, какая строка будет состоять из
нулей, то сумма элементов
, одна из строк будет
состоять из нулей. Так как заранее неизвестно, какая строка будет состоять из
нулей, то сумма элементов ![]() в каждой строке матрице
решения Х будет либо равна, либо меньше 1, а сумма элементов
в каждой строке матрице
решения Х будет либо равна, либо меньше 1, а сумма элементов ![]() в каждом столбце матрицы Х будет равна 1.
в каждом столбце матрицы Х будет равна 1.
Система ограничений примет вид:
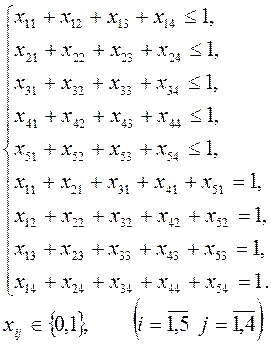
Для решения задачи необходимо перейти к закрытой модели, т.е. к исходной матрице С добавить нулевой столбец (введем 5-ю фиктивную продукцию):

Получим матрицу пятого порядка (n = 5). Дальше решаем как в задаче 3а.
а) задача максимизируется.
Для получения оптимального решения перейдем к задаче о назначении с минимизацией целевой функции:
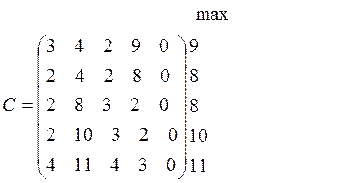
Вычитая элементы строк соответственно из чисел 9, 8, 8, 10, 11, получим матрицу C’. Затем, используя алгоритм о назначении с минимизацией целевой функции получим:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.