Радиоавтоматика: Методические указания к самостоятельной аудиторной работе, страница 10

Пример 2. Три инерционных эвена и одно идеальное дифференцирующее:

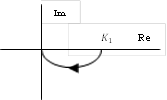
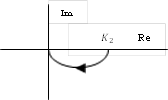
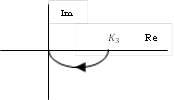
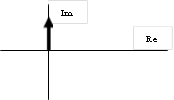
Зарисуем отдельно годографы всех четырех звеньев:

 

На частотах, равных нулю, модули коэффициентов передачи инерцион­ных звеньев-константы, фазовые сдвиги отсутствуют. У дифференци­рующего звена модуль равен нулю, фазовый сдвиг +. Следова­тельно, годограф данной цепи звеньев начинается из нуля в направ­лении + , т.е. вверх. На бесконечно больших частотах модули коэффициентов передачи инерционных звеньев стремятся к нулю, а дифференцирующего – к бесконечности. Однако в произведении этих модулей не будет неопределенности, так как инерционных звеньев три, а дифференцирующее – одно. В результате модуль коэффициента передачи рассматриваемой цепи при стремится к нулю. Что касается фазового сдвига, то три инерционных звена дадут при фазовый сдвиг , а одно дифференцирующее + . Все вместе дадут фазовый сдвиг . Следовательно, при годограф вой­дет в начало координат под углом -180°, т.е. слева. В процессе увеличения частоты от 0 до  движение точки по годографу должно осуществляться по часовой стрелке, так как все инерционные звенья плавно наращивают фазовый сдвиг в одну и ту же сторону.

Таким образом, годограф выходит из начала координат вверх по касательной к мнимой оси и, обойдя три квартала, войдет в начало координат слева по касательной к вещественной оси (рис.4.3).

 

Im

 

                                                   -1                                           Re

 

Рис.4.3

Что касается модуля усиления на средних частотах, то, как следует из формулы

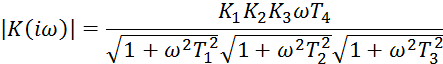
здесь имеются две тенденции - увеличение модуля за счет числите­ля и уменьшение за счет роста знаменателя. Однако числитель рас­тет линейно, а знаменатель - нелинейно. Поэтому на низких часто­тах преобладает скорость роста числителя, а на высоких - знаме­нателя. Отсюда - и такая форма годографа. Если данную цепь из 4-х звеньев охватить обратной связью и превратить в систему ав­торегулирования, то она будет устойчива при любых коэффициентах усиления и постоянных времени, так как годограф принципиально не может пересечь отрицательный отрезок вещественной оси и охватить точку (-1). Такие системы называются структурно устойчивыми.

Пример 3. Цепь из двух инерционных звеньев и одного ин­тегрирующего

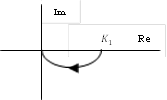
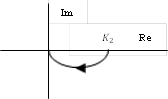
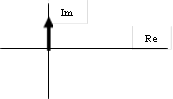
Зарисуем отдельно годографы звеньев:

 

Ситуация несколько напоминает пример I, лишь одно интегрирующее звено заменено на инерционное. Поэтому рассмотрим этот пример более коротко:

 

На средних частотах происходит плавное уменьшение модуля коэффи­циента передачи и увеличение фазового сдвига в направлении по ча­совой стрелке. Вид годографа цепи звеньев показан на рис.4.4.

                                                               Im

                                                                                   Re

 

Рис.4.4

Если рассмотренные звенья включить в состав системы автоматичес­кого управления, то вопрос об ее устойчивости не может быть ре­шен только исходя из формы годографа, так как при некоторых пара­метрах звеньев годограф может охватывать точку (-1), а при дру­гих – не охватывать. В таких случаях требуется подробный анализ по одному из критериев с выполнением необходимых расчетов.

Задачи для самостоятельного решения в аудитории

Задача 4.I.Задана структура:

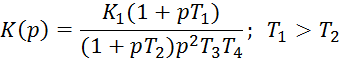
Зарисовать годограф амплитудно-фазовых частотных характеристик.

Задача 4.2. Повторить решение задачи 4.I при

Задача 4.3.

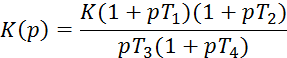
Зарисовать годограф амплитудно-фазовых частотных характеристик.

Задача 4.4. Задана структура:

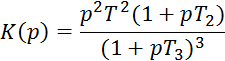
Зарисовать годограф амплитудно-фазовых частотных характеристик.

Задача 4.5. Задана структура:

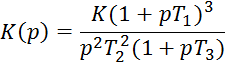
Зарисовать годограф амплитудно-фазовых частотных характеристик.

Тема 5. МЕТОД ЧЕРЕДУЮЩИХСЯ КОРНЕЙ