Дискретная оптимизация. Задачи и методы дискретной оптимизации

     Наиболее распространёнными задачами дискретной оптимизации являются.

1)  Транспортная задача – имеется  складов некоторого вида продукции с запасами  на каждом из них и  потребителей этой продукции с потребностями . Задана стоимость  перевозки единицы продукции с -го склада к -му потребителю. Требуется найти оптимальный план перевозок, т.е. величины  продукции, перевозимой с -го склада -му потребителю таким образом, чтобы стоимость перевозок (суммарная) была минимальной. В математической постановке данная задача выглядит следующим образом:

,                                                                        

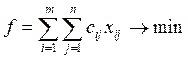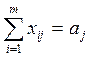 (потребности всех потребителей удовлетворены)

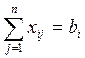  (вся продукция со складов вывезена)

 – целые.

2)  Задача о назначении – имеется  работ и  кандидатов на выполнение каждой из них. Назначение -го рабочего на -го работу сопряжено с затратами . Необходимо определить наилучшее с точки зрения минимальных затрат распределения рабочих по работам. В комбинаторном смысле данная задача представляет собой поиск оптимальной перестановки  из  элементов без повторения на всём множестве  перестановок, т.е. или

        Математическая постановка данной задачи выглядит следующим образом. Введём переменные  такие, что

                                 1, если -й кандидат назначен  на -ю работу;                                                                          

                                     0, в противном случае.                                                                                                              

Тогда необходимо минимизировать функцию 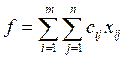   при ограничениях

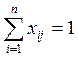
    (на -ю работу назначается только один кандидат);

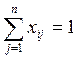
    (-й кандидат назначается на 1 и только 1 работу).

3)  Задача коммивояжёра – имеется  населённых пунктов и известны расстояния между ними [1]. Необходимо найти минимальный по длине замкнутый путь (маршрут), проходящий по всем городам по одному разу.

        Очевидно, что общее число маршрутов есть , каждый из которых представляет собой гамильтонов цикл в полном графе ² (т.е. таком графе, все вершины которого связаны с каждой).

        Математическая постановка задачи выглядит следующим образом.

Если принять, что

                                1, если путь выходит из -го города в -й;

                                0, в противном случае,

то имеем

                    ,

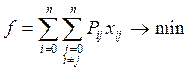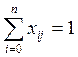
    (в каждую вершину входит одна дуга) 

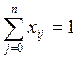
    (из каждой вершины выходит одна дуга).  

Следует отметить, что хотя минимальное значение функции  не обязательно будет целочисленным, данная задача по праву относится к задачам дискретной оптимизации по той причине, что множество допустимых решений здесь дискретно – это есть множество перестановок из  элементов без повторений.

4)  Задача о покрытии – имеется множество  элементов  и система его подмножеств . Каждому подмножеству приписан его вес  или стоимость. Требуется найти покрытие множества минимальной стоимости.

Математическая постановка данной задачи такова.

                        1, если входит в покрытие;

Пусть  

                   0, в противном случае.

Обозначим через  множество номеров тех подмножеств , которые содержат элемент .

   Для того, чтобы объединения некоторых подмножеств  было покрытием, необходимо выполнение условий ,

т.е. каждый элемент  должен принадлежать хотя бы одному подмножеству , входящему в покрытие.

5)  Задача о рюкзаке – имеется  предметов с размерами  и стоимостью , и рюкзак . Необходимо выбрать набор предметов, помещающихся в рюкзак, суммарная стоимость которых была бы максимальна. Математически это выглядит так.

                        1, если -й предмет подлежит помещению в рюкзак

Если 

                         0, в противном случае,

то   .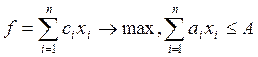

6)  Задача о расписании – имеется процессоров (рабочих станций) и  заданий на обработку. Для выполнения -ой работы на -ом процессоре требуется время . Задания взаимосвязаны, т.е. некоторые из них могут быть выполнены только после окончания выполнения других. Заданы также директивный срок  - время, в течении которого требуется обработать все задания и стоимость ожидания -ой работы до начала её выполнения. Требуется найти распределение заданий между процессорами и порядок их выполнения на каждом из них такие, чтобы общее время было минимальным (или, другой постановке, - не превышало величины ).