Метод динамического программирования (МДП)

            Метод динамического программирования (МДП) – это метод (принцип) отыскания оптимального решения задач (как с ограничениями (линейными и нелинейными), так и без них; как с непрерывными, так и дискретными переменными), обладающих свойством разложимости на подзадачи, не являющиеся независимыми. Алгоритм, основанный на МДП, решает каждую из подзадач один раз и запоминает ответ для неё в специальной таблице, для того чтобы в том случае, если на одном из последующих шагов оптимизации эта задача встретится ещё раз, можно было воспользоваться ранее полученным решением.

            Алгоритм, основанный на МДП, строится следующим образом:

–  описывается строение оптимального решения;

–  строится рекуррентное соотношение, связывающее решаемую задачу с подзадачами;

–  производится обход дерева подзадач и вычисляется оптимальное значение заданной характеристики (показателя эффективности) для каждой из них с запоминанием этих решений в таблице;

–  на основе полученной информации строится оптимальное решение.

            Согласно принципу оптимальности Беллмана, положенного в основу метода динамического программирования, оптимальная стратегия обладает тем свойством, что какими бы ни были начальное состояние и принятое начальное решение, последующие решения должны составлять оптимальную стратегию относительно состояния, которое возникло в результате первоначального решения.

            Применительно к задаче определения оптимального (максимального либо минимального) пути на графе принцип оптимальности Беллмана состоит в том, что оптимальный  путь между любыми двумя вершинами, находящимися на оптимальном пути между двумя другими вершинами, должен быть частью этого пути, или, короче, любая часть оптимального пути также оптимальна.

          Вообще, следует отметить, что задача отыскания оптимальных  путей на графе имеет многочисленные практические приложения: в задачах сетевого планирования и управления, контроля и технической диагностики, в транспортных задачах, задачах рациональной маршрутизации в распределенных вычислительных системах.

         Напомним, что путем через множество вершин (или дуг) называется такая последовательность дуг, когда конец каждой предыдущей совпадает с началом последующей. Так, если q(a_ia_j) – число из некоторого множества Q (q(a_ia_j)ÎQ), поставленное в соответствие дуге (a_ia_j) графа, где a_i,a_j – вершины графа, а числовая функция Q_s на пути S графа через вершины a_i,…,a_j,… определяется по формуле

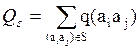                                                                      ,                                                   (1)                                                                             

то вычисление максимального пути на графе без контуров (т.е. таких, у которых имеются конечные пути, где начальная вершина первой дуги совпадает с последней вершиной конечной дуги) осуществляется на основе следующего функционального управления динамического программирования

         .                                                                      (2)

         В данном выражении – максимальное значение числовой функции на пути S из начальной вершины a₁ в вершину a_j; – множество левых инциденций для вершины a_j, т.е. множество дуг графа, для которых вершина a_j является конечной.

        Задача определения минимального пути на графе решается аналогично.

  Пусть, например, необходимо определить максимальной и минимальной пути на графе, изображенном на рис. 1, для заданных значений   дуг графа, т.е. множество Q = {1,2,3,4}, a q(2,5) = q(6,7) = 1; q(1,2) = q(4,5) = q(5,7) = 2; q(1,3) = q(3,6) = q(4,6) = 3; q(1,4) = q(3,5) = 4.

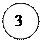
Рис. 1

            В соответствии с формулой (2) имеем:

; ; ; .

Тогда для вершины а₅ можно записать: = max[2+1;3+4;4+1] = 7. Для вершины а₆: = max[3+3;4+3] = 7. Для а₇: = max[7+2;7+1] = 9. Таким образом, максимальный путь на графе – это путь, проходящий через вершины а_1, а_4, а_6, а_7, и равный 9.  

         В то же время, жадный алгоритм решения данной задачи даёт не оптимальное, а приближённое решение, т.к. в соответствии с этим алгоритмом величина максимального пути равняется 8 (на первом шаге мы выбираем дугу между вершинами а₁ и а₄, на втором – между вершинами а₄ и а₆, на третьем – между вершинами а₆ и а₇).