Многомерные и многосвязные системы. Управление качеством переходных процессов.: Учебное пособие для курсового и дипломного проектирования, страница 9

Поскольку сложная система может быть поочередно представлена в виде одноконтурной относительно каждого выделенного эквивалента, то могут быть сформулированы методики и алгоритмы последовательного улучшения динамических свойств (в нашем случае вещественных частей характеристических корней) всей многосвязной системы. Очевидно, что итоговое качество переходных  процессов в системе на каждом последующем этапе эквивалентирования и синтеза должно контролироваться и повышаться.   

Теперь более подробно рассмотрим широко известный при исследовании и синтезе динамических свойств сложных систем формально-матричный подход. При этом отметим еще раз, что в основе математического описания системы  при любом подходе лежит модель элемента.

1.3. Методика анализа и синтеза динамических свойств сложных систем с использованием традиционных матричных моделей и методов

В основе традиционных математических моделей сложных систем лежат физические закономерности, определяющие протекание переходных процессов в различных составляющих элементах (схематично рис.1.2.4). При наличии данных о топологических связях элементов между собой (т.е. о структуре системы) может быть составлена полная система дифференциальных уравнений движения, математически описывающая совместное движение всех элементов и подсистем, с учетом их взаимного влияния. Например, на рис.1.3.1 показана структура системы дифференциальных уравнений движения сложной многомашинной электроэнергетической системы,  обобщенное представление которой приведено в п.1.2 на рис. 1.2.1. В левой части рисунка (1.3.1) цифрами 1-7 обозначены уравнения движения всех n вращающихся машин (в соответствии с рис.1.2.4). Блоки уравнений каждой машины сдвинуты относительно друг друга, что обозначает использование в каждом блоке по семь «своих» локальных переменных. Кроме этого, каждый «машинный» блок включает несколько дифференциальных уравнений Ф_i, описывающих связь регулирующих воздействий (, рис.1.2.2) с контролируемыми параметрами  (, тот же рисунок) с учетом структуры и настроечных коэффициентов «своего» АРВ-СД. Взаимосвязь блоков и локальных переменных осуществляется с помощью алгебраических уравнений сети С_i, устанавливающих граничные условия, исходя из требований соответствия значений локальных переменных параметрам установившегося режима в сети  пассивных элементов. Путем стандартных преобразований, включающих замену дифференциальных и исключение алгебраических переменных, система алгебро-дифференциальных уравнений (рис.1.3.1а) может быть приведена к матричному виду (рис.1.3.1б) или, при раскрытии матрицы A и векторов ,  и B по элементам, к виду (1.3.1).

                                                         

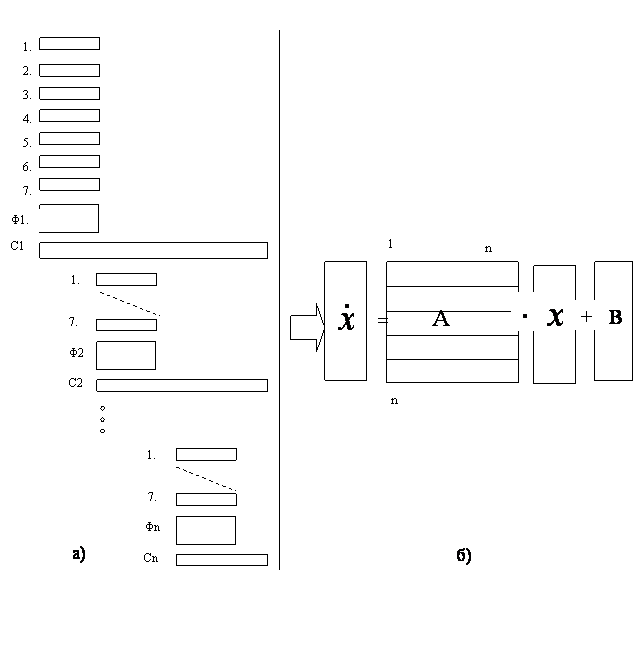
Рис.1.3.1. Схематическое изображение системы дифференциальных уравнений движения электрической системы

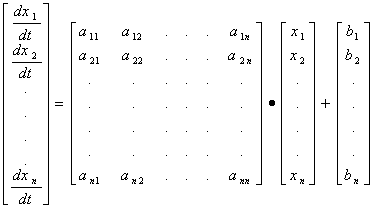   .              (1.3.1)

     .                                                               (1.3.2)

Отметим, что соотношение (1.3.1) или, что то же,  (1.3.2) формализует связь между вектором базисных (независимых) переменных  с вектором производных по времени  тех же переменных. В качестве последних могут выступать любые, входящие в исходную систему уравнений или полученные в результате действий по замене или исключению переменных. Важно, что размерность этих векторов n определяется количеством независимых дифференциальных уравнений первого порядка, соответствующих исходной системе. Очевидно, что матрица связи A, при этом является квадратной и имеет размерность (n*n). Вектор В характеризует в явном виде совокупность управляющих воздействий в системе. Как будет показано ниже, данный вектор может быть учтен в неявном виде, путем корректировки элементов матрицы A. Соотношение (1.3.2) называют записью линейных дифференциальных уравнений движения системы в форме Коши [ ], матрицу A – фундаментальной матрицей, вектор  - вектором состояния исследуемой линейной системы управления.