Многомерные и многосвязные системы. Управление качеством переходных процессов.: Учебное пособие для курсового и дипломного проектирования, страница 10

Математическая схема анализа и синтеза динамических свойств сложной системы, представленной в форме Коши, базируется на следующих рассуждениях.

Если матричное уравнение (1.3.2) не содержит правой части (т.е. отсутствует вектор управляющих воздействий) то это нерегулируемая система:

                                        .                                                (1.3.3)

В такой системе может быть выполнен лишь анализ существующих динамических свойств, поскольку изменять их без вектора управляющих воздействий невозможно. Для оценки свойств стандартными методами определяются корни характеристического определителя однородной (без правой части) системы дифференциальных уравнений (1.3.3). При этом символ дифференцирования по времени заменяют на оператор «p» (1.3.4).

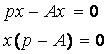                                                            (1.3.4)

Для упрощения вычисления характеристического определителя выполняются дополнительные матричные преобразования, исходя из известного положения линейной алгебры: путем элементарных преобразований любую матрицу можно свести к диагональной, при этом определитель её не изменится. Полученные диагональные элементы фундаментальной матрицы  называются ее собственными числами или характеристическими корнями матричного характеристического уравнения [p-A]  (1.3.5).

 .       (1.3.5)

Как отмечалось в п.1.1 эти собственные числа определяют конфигурацию итогового переходного процесса и, в частности, величину  исследуемого функционала качества – степени устойчивости (1.3.6).

                                                     (1.3.6)

Заметим, если раскрыть определитель (1.3.7), выполнив операцию перемножения диагональных элементов

 ,                                              (1.3.7)

то его можно привести к форме полинома:

  .                                              (1.3.8)

В задачах синтеза желаемых динамических свойств в системе должен присутствовать вектор управляющих воздействий В:

                              

Обычно компонента  управляющего вектора b_i формируется как функция от соответствующей компоненты вектора состояния x_i:

.                                                     (1.3.9)                                   

Запишем матричное уравнение в форме Коши, исключив переменные управления:

,                          (1.3.10)                        

тогда эквивалентная матрица  будет учитывать управляющие воздействия.

Тем самым показано, что фундаментальная матрица определяет новые динамические свойства исходной системы с учётом управляющих (регулирующих) воздействий. Собственные числа матрицы  полностью определяют и устойчивость и степень устойчивости системы, а значит - качество переходных процентов.

Очевидно, что задача синтеза желаемых динамических свойств сложной многосвязной системы состоит в выборе вектора соответствующих управляющих воздействий В.