Элементы зонной теории твердого тела, страница 4

Блох нашёл стационарные решения уравнения 3.4 (по модулю равна единице), а значит, волновая функция, удовлетворяющая уравнению 3.4, должна быть периодична с точностью до фазы:

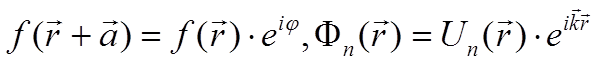       3.5

Волновая функция электрона в периодическом потенциале функция ищется в виде Блоховской волны (функция F_n(r) в выражении 3.5). Функция U_n(r) уже полностью периодическая функция (при трансляции на вектор трансляции она совпадает уже с учётом фазы). Зная потенциал V(r) можно найти функцию U_n(r), а также собственные значения e_n(). Вектор  имеет размерность импульса и называется квазимипульсом. Он имеет такой же физический смысл, как и обычный импульс, то есть сохраняется в процессах рассеяния, поглощения и рождения частиц в твёрдом теле. Приставка квази связана с тем, что определён он (как раз из за взаимодействия частиц в твёрдом теле с периодической решёткой) с точностью до вектора обратной решётки кристалла (умноженного на постоянную Планка). Постараемся пояснить это утверждение. Рассмотрим одномерный случай. Если волновой вектор  превышает , где a – период решётки, на некий вектор , то, Блоховская функция F(r) может быть записана как:

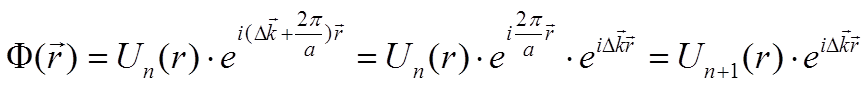
где U_n+1(r) также полностью периодическая функция. В случае, если функция U_n(r) константа, эквивалентность волновых векторов, различающихся на , проиллюстрирована на рисунке 3.2.

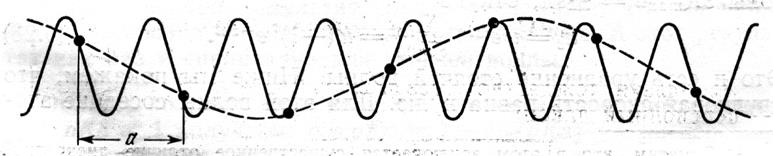
Рис. 3.2. Точками показано положение атомов.

Так как квазиимпульс определён с точностью до вектора обратной решётки, умноженного на постоянную Планка, пользуются подходом расширенных, периодических, и приведённых (свёрнутых) зон Бриллюэна, (смотри рис. 3.3.). 

Таким образом, электрон в периодическом потенциале является Блоховской волной. Достаточно плавная (для малых волновых векторов) функция  называется огибающей функцией, периодическая функция  может сильно осцилировать в пределах примитивной ячейки. Как и всякая волна Блоховская функция обладает фазовой скоростью. Вернёмся к зависимости энергии электрона от волнового вектора e_n(). Во первых, она зависит от индекса n – номера зоны. При одном и том же значении волнового вектора (и, пропорционального ему квазимпульса) возможно несколько значений энергий. Электрон при этом находится в разных энергетических зонах (валентной зоны или зоны проводимости). Зависимость энергии, а, следовательно, и частоты колебаний (e=), электрона от квазиимпульса называется дисперсией. Заметим, что дисперсия электрона в кристалле может сильно отличаться от дисперсии электрона в вакууме. Вообще говоря, Блоховская волна занимает весь кристалл. Реальный электрон, локализованный в неком месте кристалла, можно рассматривать как волновой пакет, распространяющийся с групповой скоростью. Групповая скорость определяется дисперсией (смотри, например 1.6). Таким образом, электрон в твёрдом теле это не свободный электрон, а некая квазичастица – элементарное возбуждение в твёрдом теле.

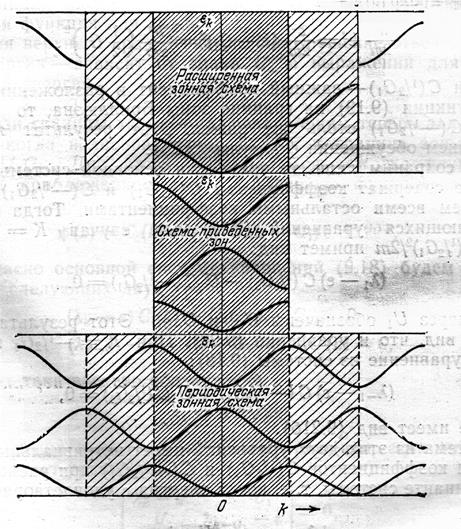
Рис. 3.3. Схемы приведённых, расширенных и периодических зон Бриллюэна.

Лекция 5. Энергетический спектр электрона в кристаллах. Дырки.

Некоторые методы расчёта электронного спектра в кристаллах. Модель почти свободных электронов. Метод сильной связи. Минимумы и максимумы энергии в спектре, долины. Эффективная масса, изоэнергетические поверхности, анизотропия эффективной массы. Понятие дырки.

Как уже упоминалось, задача нахождения усреднённого периодического потенциала V(r) сложная квантово-механическая задача, которая не имеет точного аналитического решения. За несколько десятилетий существования зонной теории твёрдого тела были развиты множество методов расчёта энергетического спектра кристаллов [2.1, 2.6-2.10]. В последнее время, в связи с развитием суперкомпьютеров, распространены «ab initio» (то есть из первых принципов) численные методы расчёта энергетического спектра. Тем не менее в них всегда присутствуют упрощения, все их можно условно разделить на 2 класса: одни из них близки к подходу почти свободных электронов, другие близки к методу сильной связи.