Специальная теория относительности. Преобразование Галилея. Опыт Майкельсона и Морли, страница 4

                                         (7)

Аналогично, при движении влево:

                                        (8)

Период, измеренный часами помещенными продольно скорости, очевидно, равен периоду измеренному часами расположенными поперечно:

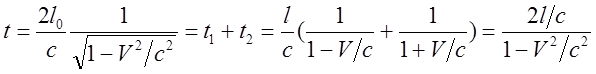       (9)

Отсюда следует, что:

                                (10)

Продольный размер движущегося стержня меньше поперечного размера . Происходит сокращение продольных размеров в движущейся системе отсчета.

Преобразования Лоренца.

Ставится  задача получить преобразования координат и времени при переходе из системы отсчета   в систему отсчета . По прежнему считается, что обе системы отсчета инерциальны,  движется в положительном направлении оси  системы . Направления осей  совпадают. Для простоты будем считать, что при  начала отсчета систем  совпадают.

По аналогии с преобразованиями Галилея будем предполагать, что искомые преобразования координат и времени  в зависимости от  линейны и имеют вид:

.

Поперечные относительно скорости движения  координаты  не преобразуются, остаются неизменными в силу сохранения поперечных размеров тел. В направлении осей  сокращения размеров не происходит. Формула преобразования времени  заранее неизвестна и будет получена аналитически. Очевидно также, что обратные преобразования, т.е. зависимости координат и времени  от   должны иметь такой – же вид с точностью до замены скорости  на . Последнее утверждение следует из принципа относительности – система отсчета  движется относительно   со скоростью  влево. Тогда:

Рассмотрим движение фронта светового импульса, испущенного при  в системе . Радиус «световой» сферы растет пропорционально времени:

Те – же соображения относительно светового фронта, распространяющегося в системе , дают:

Рассмотрим распространение световой импульса, испущенного в момент времени  из общего начала систем отсчета   вдоль оси  и  . За время  световой фронт пройдет расстояние  в системе отсчета  и  в системе . Согласно приведенным формулам:

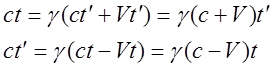
Выражая  из второго и подставляя в первое равенство,  после упрощений находим:

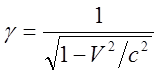                                            (11)

Определим соотношение между  и .  Воспользуемся выражениями  как функциями .

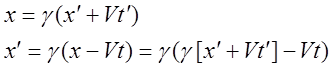
Выражая в последнем равенстве  через  и  получаем:

.

Выпишем окончательно формулы прямых и обратных преобразований Лоренца:

             

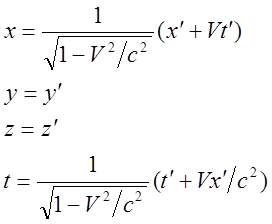
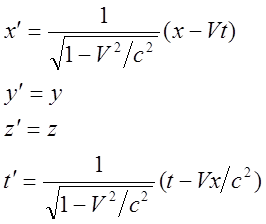
Пример. Получим формулу сокращения длины из преобразований Лоренца.

Стержень длины  покоится в системе отсчета .  Координаты концов стержня  , причем: . Координаты стержня в системе отсчета  для любого времени  определяются из преобразований Лоренца. Наблюдатель в  определит длину стержня   измерив  координаты  одновременно при . 

,  или:

что совпадает с ранее полученной формулой сокращения продольных размеров.

Релятивистские формулы преобразования скорости.

Скорости частицы, по определению, суть  в системе  и, соответственно   в системе отсчета . Требуется найти преобразования дифференциалов одних ( например нештрихованных ) величин через другие.

,                                 

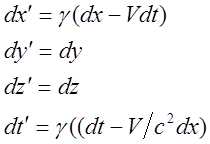
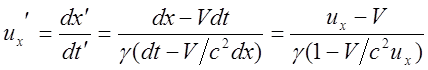Аналогично:

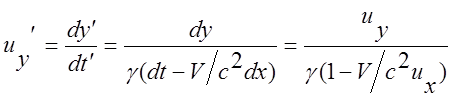,                              (12)

.                                 

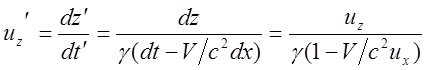Обратные преобразования отличаются заменой   на :

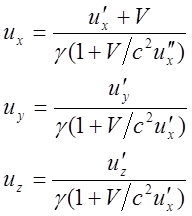                                                               (13)

Пример. Вычислить скорость относительно Земли второй ступени ракеты, выпущенной вперед со скоростью  относительно первой ступени, которая  движется со скоростью  относительно Земли. Обе скорости направлены вдоль одной прямой, которую можно выбрать в качестве осей . Итак скорость второй ступени:

.

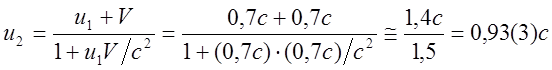В нерелятивистском  случае, согласно правилу сложения скоростей Галилея  .

В случае  формулы (12), (13) переходят в классические формулы преобразования Галилея.