Свойства потенциальных полей.
1) в области непрерывности потенциала поля u линейный интеграл не зависит от пути интегрирования и равняется приращению потенциала
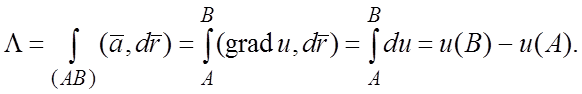 (2.3)
(2.3)
2) циркуляция (1.9) вектора ![]() по
любому замкнутому контуру, целиком лежащему в области непрерывности поля, равна
нулю:
по
любому замкнутому контуру, целиком лежащему в области непрерывности поля, равна
нулю:
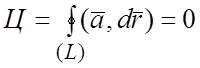 .
(2.4)
.
(2.4)
3) потенциал ![]() находится по формуле
(2.3):
находится по формуле
(2.3):
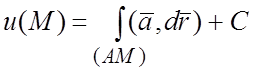 ,
(2.5)
,
(2.5)
где (AM) – произвольная кривая, стягивающая точки A и M. Если путь (AM) взять в виде ломаной, состоящей из отрезков,
параллельных осям координат (количество таких ломаных равно шести), то для
нахождения потенциала может быть применена одна из формул, выражающая потенциал
![]() через определенные интегралы
через определенные интегралы ![]() ;
; ![]() ):
):
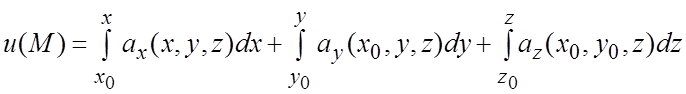 . (2.6)
. (2.6)
Пример. Проверить,
что поле вектора ![]() является потенциальным и найти
его потенциал.
является потенциальным и найти
его потенциал.
Решение. Составим для данного поля критерий потенциальности (2.2):
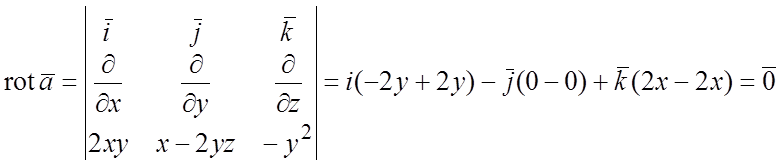
- поле потенциально. Найдем потенциал
![]() по формуле (2.6): за начальную точку
удобно взять точку A(0,0,0):
по формуле (2.6): за начальную точку
удобно взять точку A(0,0,0):
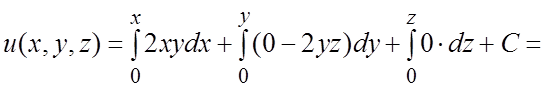
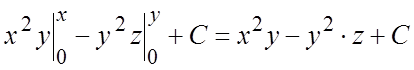 .
.
15.2.2. Соленоидальное векторное поле
Определение. Векторное поле ![]() называется соленоидальным (трубчатым)
полем, если дивергенция его равна нулю:
называется соленоидальным (трубчатым)
полем, если дивергенция его равна нулю:
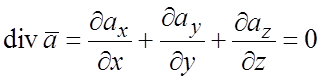 (2.7)
(2.7)
(то есть это поле без источников и стоков). Из теоремы (1.11) следует, что в соленоидальном поле поток
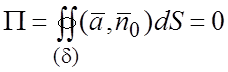 (2.8)
(2.8)
через любую замкнутую поверхность, лежащую в этом поле.
Пример. Какие из нижеследующих полей являются соленоидальными (в естественной области определения):
1) ![]() ;
;
2) ![]() ?
?
Решение. 1) вычислим
критерий (2.7): ![]() - - поле вектора
- - поле вектора ![]() соленоидально; 2)
соленоидально; 2) ![]() - поле не соленоидально.
- поле не соленоидально.
15.2.3. Дифференциальные операции второго порядка.
Лапласово (гармоническое) векторное поле
Дифференциальные
операции второго порядка – это повторно примененные операции grad, div и rot к скалярным и векторным полям, полученным в результате
применения этих же операций к скалярным ![]() и
векторным
и
векторным ![]() полям. Возможны лишь следующие повторные
операции:
полям. Возможны лишь следующие повторные
операции: ![]() ;
; ![]() ,
,
где 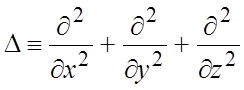 -лапласиан;
-лапласиан; ![]() ;
; ![]() ;
; ![]()
![]() .
.
Операции
первого и второго порядков удобно записывать (и вычислять, доказывать) с
помощью специального символического оператора ![]() (читается
“набла”):
(читается
“набла”):
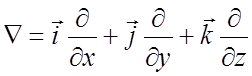 .
(2.9)
.
(2.9)
Для дифференциальных операций первого порядка имеем
![]() ;
; ![]()
![]() . (2.10)
. (2.10)
Операции второго порядка:
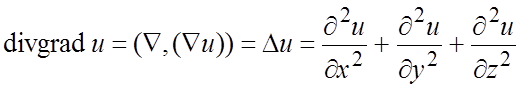 ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
При применении оператора “набла”
руководствуются следующим правилом: при применении оператора ![]() к произведениям скалярных
к произведениям скалярных ![]() ,
, ![]() ) и векторных
) и векторных
![]() ,
, ![]() полей:
полей:
![]() можно поступать так: применить оператор
можно поступать так: применить оператор ![]() к каждому из сомножителей отдельно, считая
другой постоянным (их обозначаем
к каждому из сомножителей отдельно, считая
другой постоянным (их обозначаем ![]() ), и результаты
сложить; затем каждоеслагаемое преобразовать по правилам векторной алгебра так,
чтобы оператор
), и результаты
сложить; затем каждоеслагаемое преобразовать по правилам векторной алгебра так,
чтобы оператор![]() стоял на предпоследнем месте
перед переменным множителем.
стоял на предпоследнем месте
перед переменным множителем.
Пример. Показать, что ![]() .
.
Решение. В
символической форме записи ![]() . Учитывая сначала
дифференциальный характер
. Учитывая сначала
дифференциальный характер ![]() , мы должны написать
, мы должны написать ![]() . Рассматривая выражение
. Рассматривая выражение ![]() мы можем постоянный множитель
мы можем постоянный множитель ![]() вынести за знак “набла” и, как скаляр, за
знак скалярного
вынести за знак “набла” и, как скаляр, за
знак скалярного
произведения, что дает ![]() (на последнем шаге мы
опустили индекс “c”).
(на последнем шаге мы
опустили индекс “c”).
В выражении ![]() оператор
оператор ![]() действует
только на скалярную функцию u;
поэтому мы можем написать, что
действует
только на скалярную функцию u;
поэтому мы можем написать, что ![]() . В результате получаем
формулу
. В результате получаем
формулу ![]() или
или ![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.