Переходные процессы и автоколебания релейной системы.
Рассмотрим систему с релейной характеристикой самого общего вида.
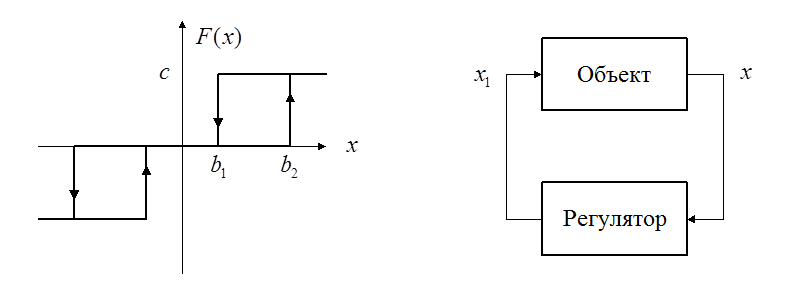
Уравнение динамики объекта: ![]() . Уравнение регулятора:
. Уравнение регулятора: ![]() .
.
Общее дифференциальное уравнение динамики системы:
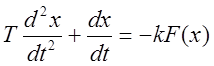 .
.
Представим это уравнение в виде:
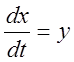 ,
, 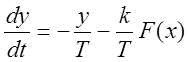 .
.
Уравнение фазовых траекторий:
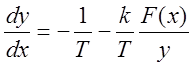 .
.
Нелинейная функция ![]() описывается следующим образом:
описывается следующим образом:
если 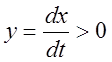 , то
, то 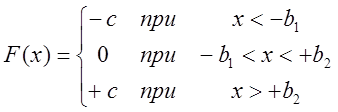 ,
,
если 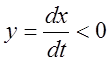 , то
, то 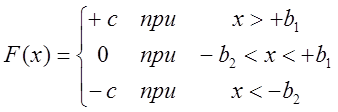 .
.
Выделим на фазовой плоскости три
области: (1) ![]() , (2)
, (2) ![]() , (3)
, (3) ![]() , разделённые так называемыми линиями
переключения (пунктирные линии на рисунке).
, разделённые так называемыми линиями
переключения (пунктирные линии на рисунке).
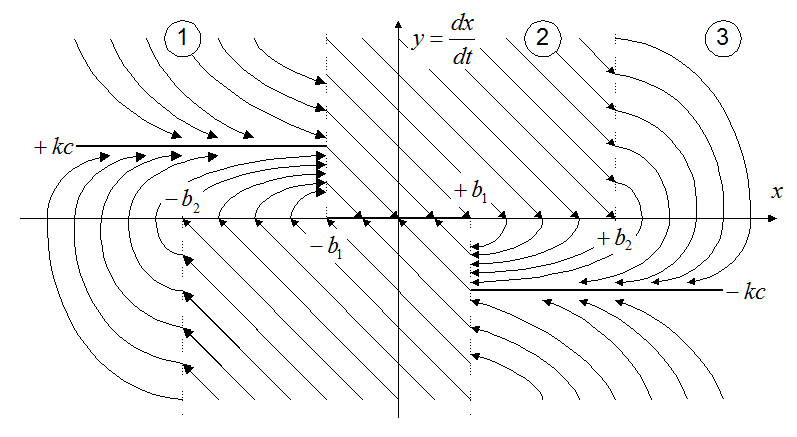
Такая фазовая плоскость называется многолистной. На каждом листе – свой вид фазовых траекторий. По линиям переключения эти листы сшиваются.
В области (1) уравнение фазовых траекторий принимает вид:
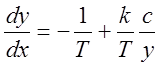 .
.
Проинтегрировав его, получим уравнение фазовых траекторий в области (1):
![]() .
.
Фазовые
траектории имеют асимптоту ![]() . Изображающая точка
движется (грубо говоря) по часовой стрелке, так как
. Изображающая точка
движется (грубо говоря) по часовой стрелке, так как ![]() –
скорость изменения x, больше нуля при
–
скорость изменения x, больше нуля при ![]() и меньше нуля при
и меньше нуля при ![]() .
.
В области (2) уравнение фазовых траекторий принимает вид:
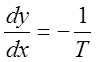 . Его решение
. Его решение 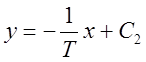 –
прямолинейные отрезки.
–
прямолинейные отрезки.
В области (3) уравнение фазовых траекторий принимает вид:
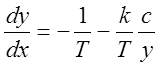 .
.
Проинтегрировав его, получим уравнение фазовых траекторий в области (3):
![]() .
.
Фазовые
траектории имеют асимптоту ![]() . Изображающая точка
движется по часовой стрелке, так как
. Изображающая точка
движется по часовой стрелке, так как ![]() – скорость изменения x, больше нуля при
– скорость изменения x, больше нуля при ![]() и
меньше нуля при
и
меньше нуля при ![]() .
.
В целом фазовые
траектории имеют форму спирали, что соответствует затухающему колебательному
процессу. Но не до нуля, а до некоторого произвольного значения в интервале ![]() . Это зона нечувствительности реле. Вместо
особой точки здесь получается особый отрезок равновесных состояний. Ход
процесса определяется начальными условиями.
. Это зона нечувствительности реле. Вместо
особой точки здесь получается особый отрезок равновесных состояний. Ход
процесса определяется начальными условиями.
Частные случаи.
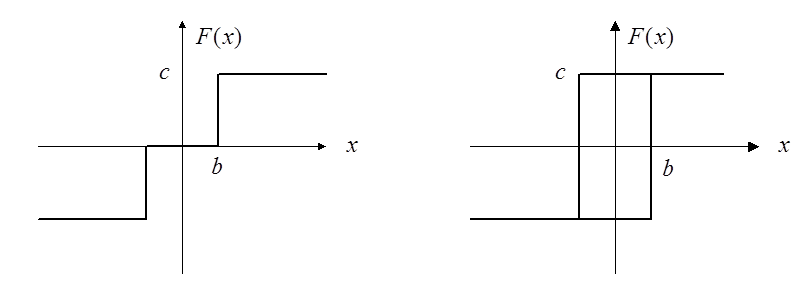
В случае
релейной характеристики с зоной нечувствительности без петель картина фазовых
траекторий аналогична описанной выше, с той разницей, что теперь ![]() .
.
В случае чисто петлевой гистерезисной релейной характеристики будет отсутствовать область (2). В этом случае
если 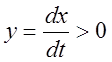 , то
, то 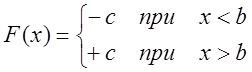 ,
,
если 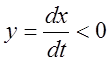 , то
, то 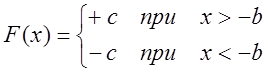 .
.
Траектории слева: ![]() , справа:
, справа: ![]() .
.
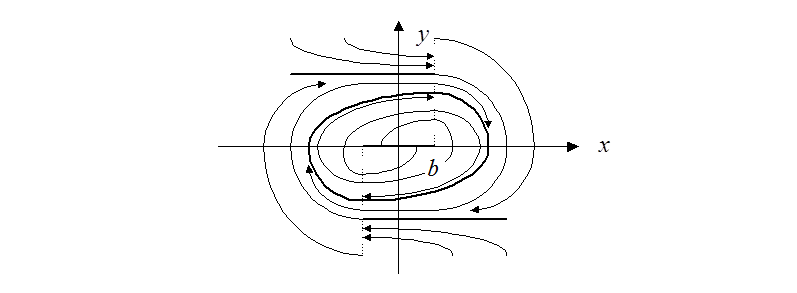
Виден устойчивый предельный цикл. Внешние траектории сходятся к нему, а внутренние – расходятся к нему. Амплитуда автоколебаний порядка b. Так работают, например, вибрационные регуляторы напряжения сети постоянного тока.
Система со скользящим процессом.
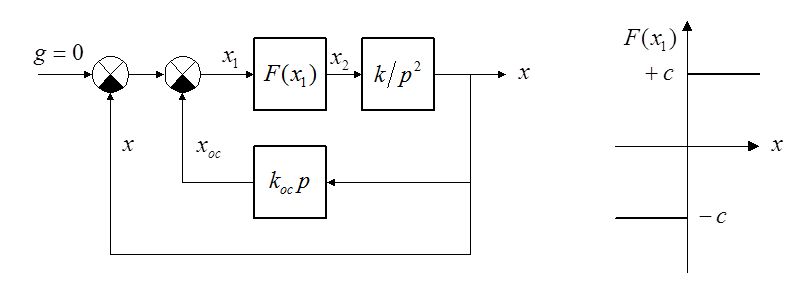
Уравнения динамики системы:
![]() ,
, ![]() ,
, ![]() .
.
В терминах дифференциальных уравнений они имеют вид:
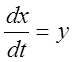 ,
, 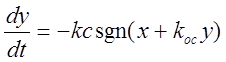 .
.
Дифференциальное уравнение фазовых траекторий:
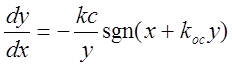 . Линия переключения
. Линия переключения 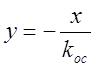 .
.
Справа от этой линии уравнение фазовых траекторий имеет вид:
![]() , откуда
, откуда ![]() –
параболы рогами налево.
–
параболы рогами налево.
Слева от этой линии уравнение фазовых траекторий имеет вид:
![]() , откуда
, откуда ![]() –
параболы рогами направо.
–
параболы рогами направо.
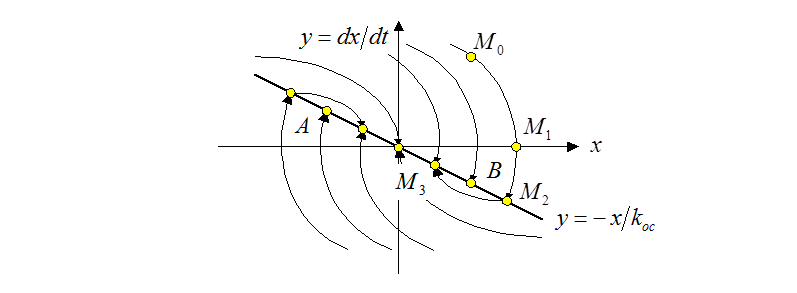
На отрезке AB
линии переключения ![]() фазовые траектории встречаются,
но движение не прекращается, так как на этой линии скорость не равна нулю:
фазовые траектории встречаются,
но движение не прекращается, так как на этой линии скорость не равна нулю:
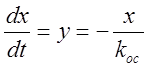 .
.
Решением этого уравнения является экспоненциальное скользящее движение:
![]() .
.
Здесь значения ![]() и
и ![]() относятся
к моменту попадания изображающей точки на линию так называемого скользящего
процесса.
относятся
к моменту попадания изображающей точки на линию так называемого скользящего
процесса.
Реально такой процесс соответствует переключению реле с большой частотой.
Отметим следующее. Нелинейная система второго порядка на участке скользящего процесса вырождается в линейную систему первого порядка. При этом закон движения не зависит от параметров прямой цепи системы и определяется только коэффициентом обратной связи.
Найдём положение концов отрезка скользящего процесса A и B. В этих точках касательные к параболам совпадают с линией переключения, то есть
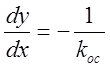 .
.
Из уравнения для фазовых траекторий получим:
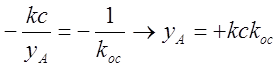 ,
, 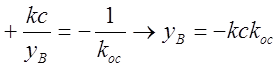 .
.
Следовательно, отрезок скользящего процесса тем больше, чем больше коэффициенты усиления прямой цепи и обратной связи.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.