Интегрируемость в квадратурах. Линейные уравнения высших порядков, страница 2

Замечание. Полученные в а) и б) результаты согласуются с общей теорией, так как исходное уравнение равносильно двум:  и . В случае а) для каждого из этих уравнений в окрестности начальной точки (0; 0; 2)  выполняются условия теоремы существования и единственности, а в случае б) эти условия не выполняются ни в какой окрестности начальной точки (0; 0; 1) – производные от правых частей по  обращаются в бесконечность при .

3)         Уравнение, не содержащее независимой переменной

          Уравнение вида

                                                                                                (5.11)

допускает понижение порядка на единицу, если ввести новую искомую функцию:  и принять y за независимую переменную . При этом производные  преобразуются так:

                                                      ;

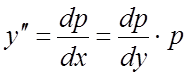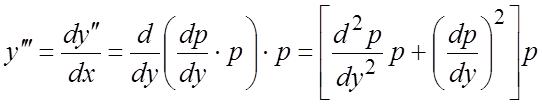                                                   (5.12)

                             ………………………………………………….

Подставляя эти выражения вместо … в уравнение, придем к дифференциальному  уравнению (n-1) – го порядка.

Замечание. Принимая y за независимую переменную, мы могли потерять решение вида . Непосредственной подстановкой  в уравнение (5.11) можно выяснить, имеет ли оно решения такого вида.

Пример 4. Решить уравнение .

Решение. Уравнение не содержит независимое переменное x. Полагая ,  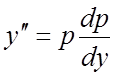, приходим к уравнению первого порядка  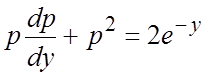- уравнению Бернулли, решаемому, например, с помощью подстановки :

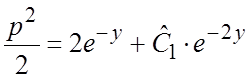, откуда 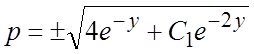. Заменяя здесь p на , разделяя переменные и интегрируя, будем иметь 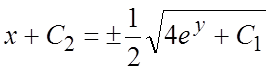. Подставляя
y = C в уравнение, убеждаемся, что y = C не является его решением.

Пример 5. Проинтегрировать уравнение

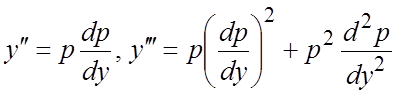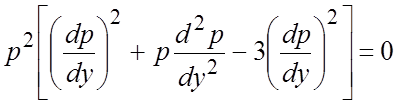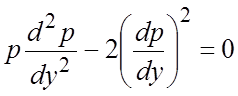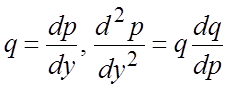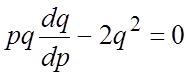Решение. Положим ; тогда . Уравнение преобразуется к виду . Приводя  подобные члены и сокращая на  (при этом следует учесть теряемое решение  ()), получим . Это дифференциальное уравнение рассматриваемого типа (5.11) (не содержит в явном виде “независимую” переменную y). Полагая здесь , придем к уравнению . Сократив на (при этом следует учесть еще одно решение , то есть  и ), получим 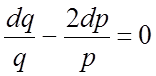, откуда  или 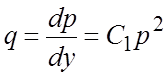. Интегрируя последнее уравнение, находим 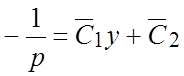, или 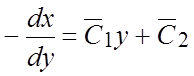. Окончательно получим , где 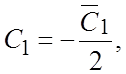 . Заметим, что в общее решение входят решения вида  .

Замечание. Может случиться, что уравнение принадлежит и к типу (5.10) и (5.11); например, это уравнение 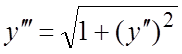. При их интегрировании предпочтение отдают методу, с помощью которого решение определяется проще; в данном примере следует считать, что это уравнение типа (5.10).

Задачи для самостоятельного решения

Найти область существования и единственности решения уравнения:

96. 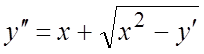;        97..

Показать, что данные выражения при любых действительных значениях входящих в них параметров определяют решения соответствующих дифференциальных уравнений:

98.

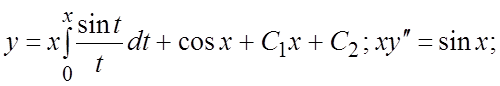
99.;   100..

Показать, что данные функции являются общими решениями соответствующих уравнений:

101.   102..

Найти общие решения (интегралы) уравнений; там, где указано, найти частные решения уравнений при заданных начальных условиях:

103.    104.     105. ;    106. ;

107.     108.;

109.     110.;  111.

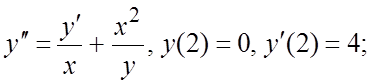
112.  113.;    114.;    115.;

116.;   117. ,

;  118.;   119.   120.;

121.;   122.;    123..

10.6.    Линейные уравнения высших порядков

10.6.1. Введение

1^°. Однородное уравнение (ОЛДУ). Линейным уравнением n - го порядка называется уравнение вида

                          ;                 (6.1)

 называются коэффициентами уравнения, - правой частью (6.1).

Определение 1. Если при всех рассматриваемых значениях x функция , то уравнение (6.1) называется однородным (ОЛДУ); в противном случае оно называется неоднородным (НЛДУ).

Теорема 1. Если коэффициенты  и  непрерывны в интервале (a,b), то для любых начальных условий (2.1) задача Коши имеет решение и оно единственно.

Всякое решение уравнения (6.1) является частным решением, так что особых решений оно не имеет.