Динамика твердого тела. Изменение момента импульса равняется моменту силы, страница 2

.                                                  (9)

Итак, для нахождения следует учитывать компоненты радиус вектора и силы, лежащие в плоскости . Точно также для определения момента импульса вдоль некоторой оси следует учитывать только компоненты радиус вектора и импульса в направлении перпендикулярном оси:

                                        (10)

Из приведенных соотношений следует простое правило вычисления момента силы относительно некоторой оси. Следует умножать перпендикулярную относительно выбранной оси составляющую силы на плечо – которое является кратчайшим расстоянием от оси и линией действия силы (см. рис n5).

Момент импульса материальной точки, вращающейся вокруг фиксированной оси.

Выберем в качестве заданной неподвижной оси – ось вращения материальной точки. Частица массы  движется по окружности радиуса  в плоскости перпендикулярной оси вращения (см. рис. n7). Согласно определению момент импульса частицы . Введем угловую скорость вращения частицы , тогда . Подставляя в выражение для момента импульса имеем: . Для системы частиц, вращающихся относительно выбранной оси с одинаковыми угловыми скоростями имеем:

                            (11)

Сумма произведений масс частиц на квадраты расстояний относительно выбранной оси называется моментом инерции тела относительно оси - . Момент импульса тела относительно оси равен произведению момента инерции относительно выбранной оси на угловую скорость (11).

Основное уравнение динамики твердого тела (8), вращающегося относительно выбранной оси с учетом переписывается в виде:

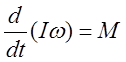                                                  (12)

Если ось вращения твердого тела (недеформируемой системы материальных точек) неподвижна, то момент инерции величина постоянная, тогда:

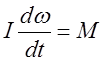                                          (13)

- по определению есть угловое ускорение, следовательно: произведение момента инерции относительно некоторой оси на угловое ускорение равно моменту сил относительно этой оси.

Существует аналогия между величинами и формулировкой законов динамики поступательного движения частицы и величинами и формулировкой законов динамики вращения. В самом деле: линейной координате сопоставляется угол , линейной, поступательной скорости  ставится в соответствие угловая скорость, силе - момент силы , импульсу - момент импульса , продолжая аналогию можно утверждать, что массе соответствует момент инерции . В формулировках основных законов динамики поступательного движения и динамики вращения очевидна точная аналогия. Сравнение формулировок законов изменение импульса равно силе и изменение момента импульса равно моменту силы доказывает этот факт.

Работа при элементарном повороте.

Рассмотрим вращение частицы массы в некоторой плоскости по окружности некоторого радиуса . Восстановим ось вращения – перпендикуляр проходящий через центр окружности. Подсчитаем работу, совершенную внешней силой при малом повороте частицы относительно оси.

Определим кинетическую энергию твердого тела, вращающегося относительно заданной оси:

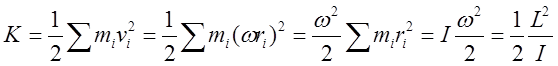              (14)

Записывая основное уравнение динамики вращения в дифференциальной форме:  и, находя малое приращение кинетической энергии вращения:

убеждаемся, что , как в случае поступательного движения.

Примеры вычисления момента инерции.

1. Момент инерции массивного массы  бесконечно тонкого кольца радиуса относительно оси вращения, проходящей через центр.

Считаем, что ось вращения перпендикулярна плоскости кольца. Разбивая кольцо на точечные массы и, суммируя все вклады , находим:

2. Момент инерции однородного диска массы , радиуса  относительно оси, проходящей через центр (монета).

Разбивая диск на семейство бесконечно тонких колец радиуса от  до и суммируя затем все вклады находим (- плотность диска на единицу площади ):

3. Момент инерции однородной палочки (линейная плотность ), вращающейся относительно оси, проходящей через конец.

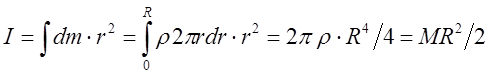
Воспользовавшись определением: .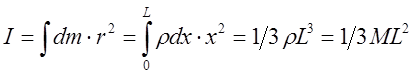

4. Момент инерции однородной палочки, вращающейся относительно оси, проходящей через центр масс.

Аналогично предыдущему примеру: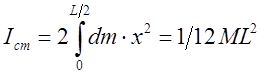  

Оказывается . Разница составляет , где - расстояние между центром масс и концом палочки.

Теорема Штайнера.

Момент инерции относительно произвольной оси равен моменту инерции относительно оси проходящей через центр масс, параллельной первой плюс произведение массы тела на квадрат сдвига между осями.