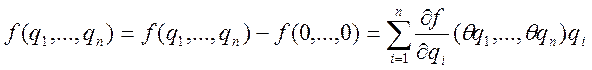Обобщенные средние функции. О соотношении цены и качества, страница 2

       ,   где ,         (9)

Следовательно, в силу 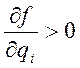, имеем следующие оценки:

,

.

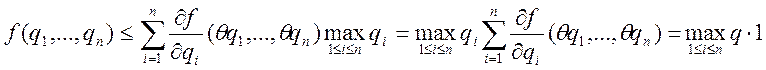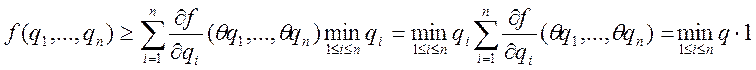          Что и требовалось доказать. 

          Таким образом, все НС действительно являются средними функциями.

 Простейшим примером  НС является любая функция вида (1) при условии, что все . Другой пример получается  из средних по Колмогорову-Нагумо функций  

 ,

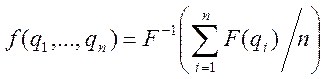где   -  любая монотонная функция. В качестве  выберем любую функцию вида  ,  ,  .  Тогда    

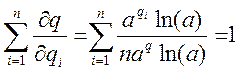 ,  т.к. .

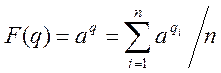В силу определения 3, функция  является нормализованной средней (НС).

         Следующая теорема описывает содержательное свойство НС, которым

обусловлена привлекательность таких функций, рассматриваемых с точки зрения проблемы свертывания частных показателей качества в единый (показатель). 

Теорема.  Если -  нормализованная средняя функция,  то при 

,  ,     необходимо  имеет место  ,  где ,    .               

          Доказательство.   По формуле конечных приращений Лагранжа имеем:

,

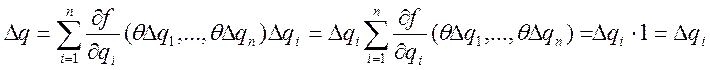что и требовалось доказать. 

         Таким образом, при равном изменении каждого из рейтингов объекта по всем его частным качествам,  единый рейтинг (по всем качествам в совокупности) изменится ровно на столько же позиций. 

          Рассмотрим примеры, в которых  НС являются многочленами. Они представляют собой новые,  ранее не известные средние функции.

          Пример 1.   Многочлен 2-й степени

,  где ,

,     .

Последние два неравенства эквивалентны условию строгой монотонности.

         Пример 2.  Многочлен 3-й степени

 ,  где

и коэффициенты  удовлетворяют хотя бы одной из двух систем неравенств:

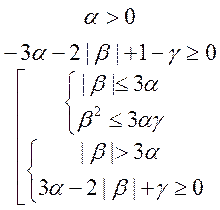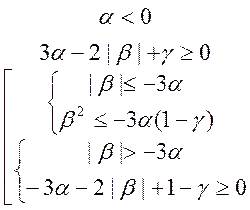                                или                      (10)

Эти  две системы, в совокупности, эквивалентны строгой монотонности.

         Аналогично можно получить многочлен любой степени по переменным , являющийся  НС.  Для этого достаточно выписать его с неопределенными коэффициентами и подставить в следующее уравнение :

 .

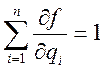С учетом условия , отсюда получится система линейных уравнений относительно коэффициентов многочлена, из которой эти коэффициенты и определятся (неоднозначно). Например, многочлен 4-й степени, являющийся НС двух аргументов, выглядит так:

 

Следует позаботиться о монотонности

                                          ,    ,    ,                                       

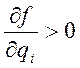которая накладывает на коэффициенты многочлена дополнительные условия. 

         В общем процедура использования нормализованных средних функций может быть следующей.

         Выделим один из частных показателей качества, например , свертывание которого в единый показатель  наиболее затруднительно.

Вначале следует определить функцию  , которая выражает  через показатели  в предположении, что  .  Для задания функции , однако, следует использовать нечеткие (fuzzy) методы усреднения показателей качества  [8].  Они остаются актуальными, хотя уровень неопределенности задачи при использовании НС   несколько снижается.  Затем решается задача Коши для уравнения

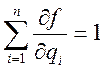    с начальным  условием  .         

По теореме Коши-Ковалевской  в случае, когда функция  является аналитической, данная задача Коши хотя бы локально имеет единственное аналитическое  решение.  Если  при всех , то получена искомая  НС

.

Лекция

О соотношении цены и качества.