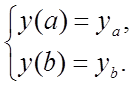 (11.11)
(11.11)
У такий спосіб необхідна умова екстремуму функціонала I(y) у класі функцій із закріпленими кінцями зводиться до крайової задачі для диференціального рівняння.
Будь-яке рішення рівняння (11.10) називається екстремаллю функціонала I(y).
Окремі випадки рівняння Ейлера :
1 Функція F=F(x,y/) не залежить від у.
З рівняння (11.10) очевидно,що ![]() , отже,
, отже,
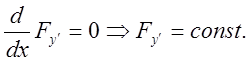
2 Функція F=F(y,y/) не залежить від x.
Знижуємо порядок і з рівняння (11.10) одержуємо
F-y/Fy/=const.
3
Функція F=f(x,y) не
залежить від ![]() . Тоді рівняння Ейлера - це
. Тоді рівняння Ейлера - це
алгебраїчне, а не диференціальне рівняння.
Приклад . Задача про брахістохрону. З точки А до точки В під дією сили тяжіння скочується точка масою m .Серед усіх неперер-вних функцій, що з’єднують ці точки, знайти ту, за якою точка скотиться за найменший інтервал часу.
Позначимо s-шлях, v- швидкість , t – час руху точки по кривій y(x). За законами фізики
ds=vdt , ![]() => dt=
=> dt=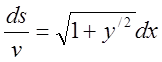 ,
,
v=![]() (закон Галілея); dt=
(закон Галілея); dt=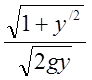 dx.
dx.
Час руху точки вздовж кривої y(x) можна визначити як
t(y)=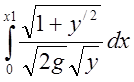 .
.
Оскільки від const функціонал
не залежить, то ![]() відкидаємо і одержуємо функціонал,
що будемо мінімізувати
відкидаємо і одержуємо функціонал,
що будемо мінімізувати 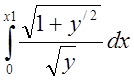 .
.
Підінтегральна функція
F(x,y,y/)=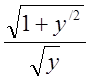 не залежить від х, отже,
використовуємо окремий випадок рівняння Ейлера
не залежить від х, отже,
використовуємо окремий випадок рівняння Ейлера
![]() =const.
=const.
Для
даної функції![]() =
=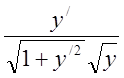 і рівняння Ейлера має
і рівняння Ейлера має
вигляд
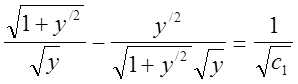 .
.
Проводячи спрощення, отримуємо
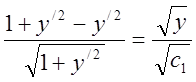 =>
=> 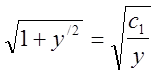
![]() 1+y/2=
1+y/2=![]() .
.
Остаточно маємо
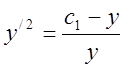 - це рівняння
Лагранжа.
- це рівняння
Лагранжа.
Інтегруємо в параметричній формі за допомогою заміни 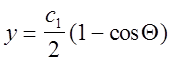 . Підстановка її в рівняння надає вигляду
. Підстановка її в рівняння надає вигляду
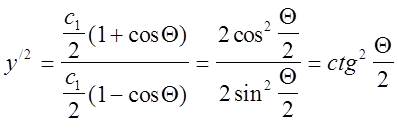
![]()
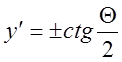 ,
,
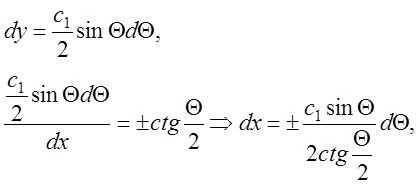
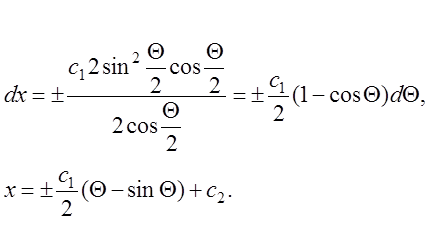
Остаточно одержуємо рівняння множини кривих в параметрич-ній формі
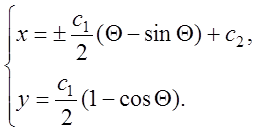 (циклоїда)
(циклоїда)
Оскільки
крива проходить через точку А(0,0) то в ній кут ![]() =0,
c2=0:
=0,
c2=0:
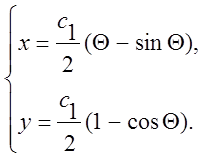
Значення
![]() в точці В(x1 y1)
і const с1 визначаються з умови
в точці В(x1 y1)
і const с1 визначаються з умови
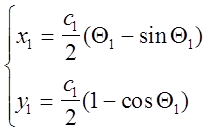 =>
=> 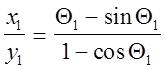 .
.
Значення
![]() знайдемо, використовуючи методи розв’язання нелінійних рівнянь (ітераційні, наприклад). Згодом можна визна-чити і с1 із
системи
знайдемо, використовуючи методи розв’язання нелінійних рівнянь (ітераційні, наприклад). Згодом можна визна-чити і с1 із
системи 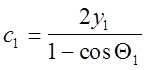 .
.
У такий спосіб рівняння екстремалі знайдено.
11.3 Екстремаль функціонала, що залежить від похідних вищого порядку
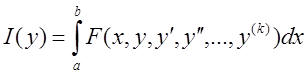 . (11.12)
. (11.12)
Розглянемо проблему пошуку екстремалі
функціонала на класі функцій ![]() із закріпленими кінцями
на проміжку
із закріпленими кінцями
на проміжку ![]() . Сюди входять функції, що разом з
. Сюди входять функції, що разом з ![]() своїми похідними неперервні на
своїми похідними неперервні на![]() і для них визначена норма
і для них визначена норма
![]() . (11.13)
. (11.13)
Для пошуку екстремалі у цьому випадку треба використати рівняння Эйлера-Пуассона
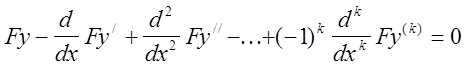 . (11.14)
. (11.14)
Це рівняння ![]() 2-го порядку ,до нього необхідно додати
граничні умови:
2-го порядку ,до нього необхідно додати
граничні умови:
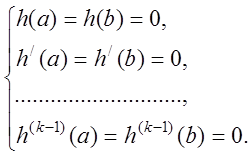 . (11.15)
. (11.15)
Тут ![]() -
варіація функції (
-
варіація функції (![]() ),
),
![]() -
варіації її похідних.
-
варіації її похідних.
Приклад. Знайти екстремаль
функціонала серед функцій класу![]() із закріпленими кінцями:
із закріпленими кінцями:
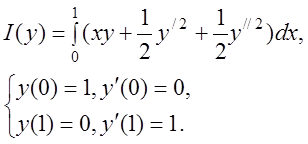
Складемо рівняння Ейлера-Пуассона: ![]()
![]()
![]()
![]()
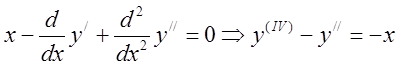 .
.
Отримали лінійне неоднорідне диференціальне рівняння 4-го по-рядку з постійними коефіцієнтами. Знаходимо корені його харак-теристичного рівняння:
k2(k2-1)=0 ; k1,2=0 ;
k3,4=![]() .
.
Загальний розв’язок
y=c1+c2x+c3shx+c4chx+![]() ,
,
де довільні
константи ![]() визначаємо з граничних умов.
визначаємо з граничних умов.
Завдання 12 Знайти экстремаль функціоналу в класі функцій ![]() з
закріпленими кінцями:
з
закріпленими кінцями:
1 I(y)=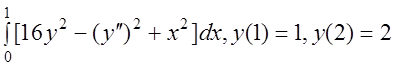 .
.
2 I(y)=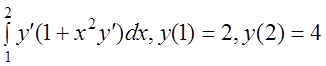 .
.
3 I(y)=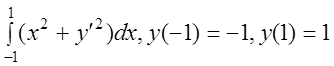 .
.
4 I(y)=2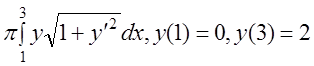 .
.
5 I(y)=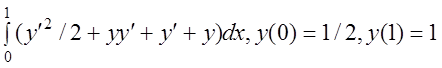 .
.
6 I(y)=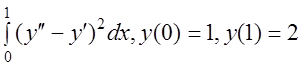 .
.![]()
7 I(y)=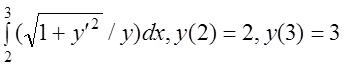 .
.
8 I(y)= 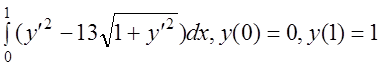 .
.
9 I(y)=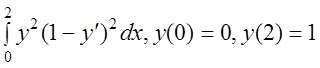 .
.
10 I(y)=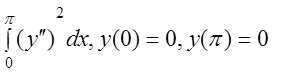 .
.
11 I(y)=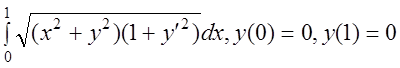 .
.
12 I(y)=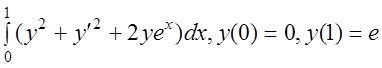 .
.
13 I(y)=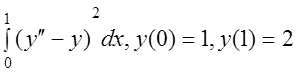 .
.
14 I(y)=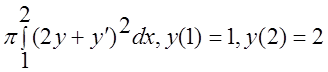 .
.
15 I(y)=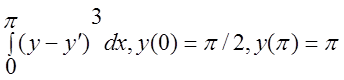 .
.
16 I(y)=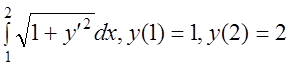 .
.
17 I(y)=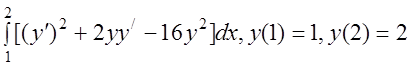 .
.
18 I(y)=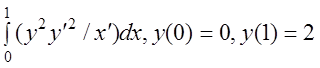 .
.
19 I(y)=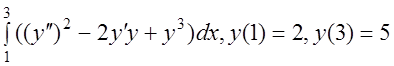 .
.
20 I(y)=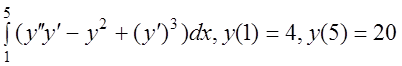 .
.![]()
21 I(y)=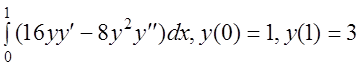 .
.
22 I(y)=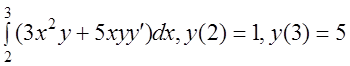 .
.
23 I(y)= 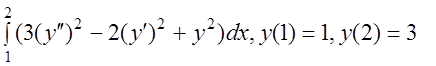 .
.
24 I(y)=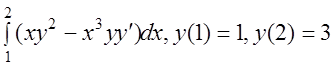 .
.
25 I(y)=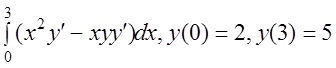 .
.
26 I(y)=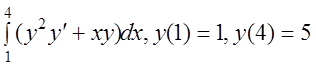 .
.
27. I(y)=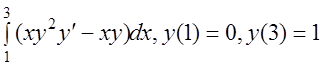 .
.
28 I(y)=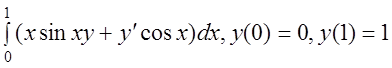 .
.
29 I(y)=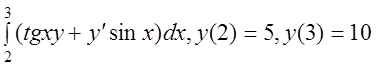 .
.
30 I(y)=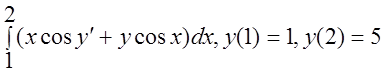 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.