Чисельний пошук екстремуму функції однієї змінної. Чисельні методи пошуку екстремуму функції декількох змінних, страница 3

Ітераційний процес методу градієнтного спуску будується за формулою

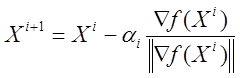,                           (10.3)

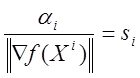
 -число;

 відповідає властивості (градієнта);

крок роблять у напрямку, протилежному вектору градієнта, у бік максимального спадання функції.

Різні стратегії вибору кроку  визначають різні варіанти градієнтного спуску:

-  найшвидшого спуску,

-  зменшення кроку.

Метод найшвидшого спуску для пошуку розв’язку передба-чає такі процедури :

1  Вибираємо початкову точку , обчислюємо градієнт , коли , то точка  - стаціонарна, процес закінчений.

Якщо , то підставляємо в (2.1)  i=0 і отримуємо пер-шу точку за формулою

 .

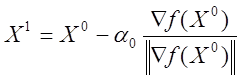Функція при заданому  є функцією тільки . Мінімі-зуємо  за .З умови мінімуму знаходимо . Визначаємо точку і знову перевіряємо . Якщо ,то точка  стаціонарна, процес закінчений, коли ні, то підставляємо у формулу (2.1) , переходимо на наступний крок і т.д.

2  Призначають точність >0, процес припиняють, як тільки ви-конуються співвідношення

.

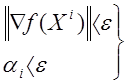За точку мінімуму береться  на останньому кроці .

Недоліки методу : задача мінімізації функції при визначенні  на кожному кроці вимагає застосування чисельних методів розв’язку нелінійних рівнянь, що потребує громіздких обчислень.

На практиці часто користуються методом градієнтного спуску зі зменшенням кроку дослідним шляхом. Тобто відбуваєть-ся спуск при довільному , і на кожному кроці процесу перевіряємо умову монотонності   Якщо ця умова порушується, то  зменшується до тих пір, поки монотонність не відновиться .

Приклад.Знайти мінімум функції методом найшвидшого спуску.

,       ,

,,

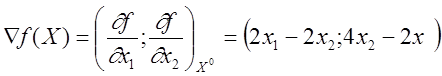норма градієнта . Точка - нестаціона-рна, тому що . Треба будувати ітераційний процес. Беремо  і шукаємо першу точку :

 = ,

;

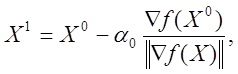
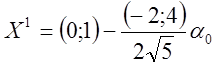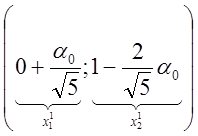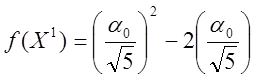
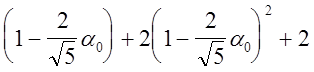мінімізуємо  за  :

;

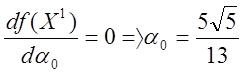підставимо і одержимо.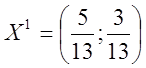

Знайшли , пішли на наступний крок :; знайшли наступну точка  і т.д.

Точний мінімум :.

Завдання 11. Методом градієнтного спуску знайти мінімум функції при заданій початковій точці.

1  .

2  0.

3  .

4  .

5  .

6  .

7 

8 

9 

10 

11 

12 

13 

14 

15 

16 

17 

18 

19 

20 

21 

22 

23 

24 

25 

26 

27 

28 

29 

Глава 11

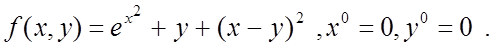
 Варіаційне числення

У попередній главі розглядалися задачі на максимум та мі-німум процесів, які можуть бути описані функціями зі скінченним числом змінних. Основна задача варіаційного числення полягає у розробці методів розв’язання задач на екстремум процесів, що опи-суються функціями з нескінченним числом змінних. У цьому ви-падку максимуми і мінімуми досягаються на лініях, поверхнях і тому подібне, тобто на функціях. Якщо у першому випадку стаціо-нарні значення ( точки екстремуму) визначаються з алгебраїчних або трансцендентних рівнянь, то у другому випадку функції визна-чаються з диференціальних рівнянь.

Як відомо, поняття функції пов’язане з можливістю встанов-лення відповідності між двома множинами чисел, одна з яких на-зивається аргументом, а інша - функцією.

Поняття функціонала пов’язане з відповідністю між множи-ною певного класу функцій та множиною чисел, а саме: якщо кожній функції певного класу ставиться у відповідність за деяким законом певне числове значення змінної  то цю змінну називають функціоналом від однієї функціональної змінної і позначають . За цим визначенням функція  є незалеж-ною змінною для функціонала. Областю визначення для функціонала є певний клас функцій.