Застосування теорії чисел в криптографії, страница 9

Доводити будемо побудовою числа . Позначимо через  НСК всіх модулів. Оскільки вони попарно прості, то . Далі побудуємо систему чисел

Кожне  є взаємо простим з числом , тому для нього існує обернений елемент

Побудуємо число: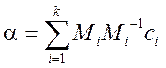

Тоді розв’язком системи (2) буде клас лишків, що задовольняє конгруенції:

Дійсно, підставимо  у першу конгруенцію системи (2):

Всі доданки, починаючи з другого діляться на , бо цей модуль присутній у , як множник. Тому всі ці доданки конгруентні 0 за модулем . Добуток  за побудовою, . Залишається тотожна конгруенція .

У другому рівнянні не конгруентно 0 за модулем  тільки доданок . Отже  є розв’язком для другої конгруенції і т. д.

Розв’язок підійде до кожної конгруенції в силу своєї структури.

Висновок: Розв’язок системи (2) існує, і це є клас чисел

Приклад. Розв’язати систему конгруенцій.

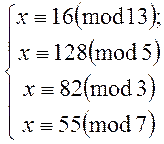
Розв’язання. По-перше спростимо систему:

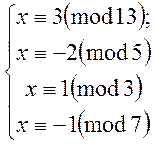
Знайдемо обернені значення до :

            

            

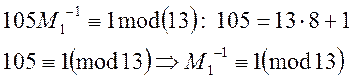
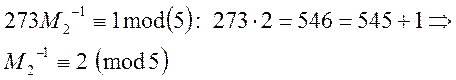
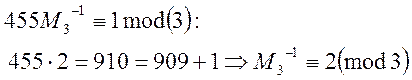
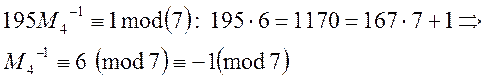
Будуємо розв’язок:

Перевірка:

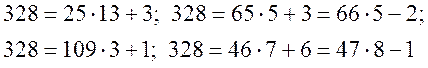
Система розв’язана вірно.

Відповідь: розв’язком системи є клас лишків  за модулем, що дорівнює НСК 13, 5, 3, 7

Якщо у системі (1) для будь якої конгруенції  , то скорочуючи конгруенцію на , переходимо до конгруенції 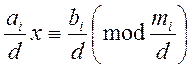 і вже цю конгруенцію підставляємо до системи. Якщо для нової системи збереглася попарна простота модулів, то вона має єдиний розв’язок, згідно з китайською теоремою про залишки. Але в цьому випадку -та конгруенція має  розв’язків: 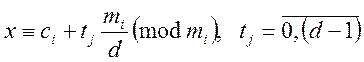, отже необхідно розглянути, відповідно,  систем, в кожній з яких на му місці буде стояти відповідний розв’язок конгруенції.

Якщо модулі системи конгруенцій не є попарно простими, тобто , то для розв’язання системи треба додатково досліджувати існування розв’язку. Якщо він є, то це буде розв’язок за модулем, рівним НСК модулів системи: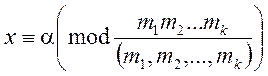

Розглянемо для прикладу систему з двох конгруенцій. Будемо вважати, що її можна звести до вигляду:

Нехай

Будемо розв’язувати систему методом підстановки. З першої конгруенції можна записати:

. Розв’язок повинен задовольняти і другу конгруенцію. Підставимо  у другу конгруенцію:

Отже виникла умова: Якщо , то друга конгруенція розв’язок має. В іншому випадку – ні.

Нехай умова виконується. Тоді розглядаємо конгруенцію 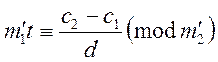. Розв’язком

її буде конгруенція 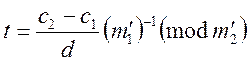. Розв’язок можна подати:

.

Підставимо значення  у вираз для :

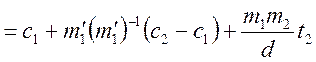
Позначимо 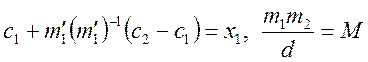. Тоді розв’язок системи буде мати вигляд:

Висновки. 1.Система з двох рівнянь виду  в разі  буде мати розв’язок тільки за умови, що . В іншому разі система не сумісна. Якщо умова виконана і розв’язок є, він буде знайдений за модулем, який дорівнює НСК  та

2. Якщо система складається з  конгруенцій з модулями, що мають НСД>1, то перевірку необхідно проводити поступово. В разі, коли хоча б одна з отриманих конгруенцій в ході розв’язку немає розв’язку, то і вся система не сумісна. Якщо розв’язок є, то це буде конгруенція по НСК усіх модулів.

5. Конгруенції n-го степеня.

5.1 Конгруенції n-го степеня за простим модулем.

Розглянемо загальні теореми, які стосуються конгруенцій n-го степеня за простим модулем . Припустимо, що задано конгруенцію

,                                                     (1)

де  - просте число і  не ділиться на .

Теорема 1. Конгруенцію (1) завжди можна замінити на еквівалентну їй

Справді, через те що  — просте і  не ділиться на  завжди існує єдине число, обернене до : . Помноживши конгруенцію (1) на , отримаємо еквівалентну конгруенцію із старшим коефіцієнтом

Теорема 2. Якщо степінь конгруенції (1) не менший від модуля конгруенції, то вона еквівалентна деякій конгруенції степеня, не вище за (за тим самим модулем). Тобто, якщо у (1) , то

Доведення.

Поділимо на . Частку від ділення позначимо через, залишок – через . Тоді на підставі алгоритму ділення з остачею дістанемо:

де  – поліном, степеня ,  – поліном степеня, не більшого за . Коефіцієнти ,  – цілі числа. За теоремою Ферма якщо  – просте число, то  для будь-якого цілого х. Отже, отримаємо еквівалентну конгруенцію:

Висновок: Конгруенції  та  мають однакові корені.

Частинні випадки:

1. . Тоді  - тотожна, , тобто вірна для будь якого .