Практическое занятие №2 (ТСО).
Цель занятия :Ознакомиться с простейшими арифметическими алгоритмами и методами оценки их сложности.
Для удобства
мы будем полагать, что мы оперируем с целыми числами, выраженными в двоичной
системе счисления. У нас есть два ![]() - разрядных числа
- разрядных числа ![]() и
и ![]() , то
можно записать
, то
можно записать
![]()
где ![]() - ²
наиболее значимая половина ² числа
- ²
наиболее значимая половина ² числа ![]() , а
, а ![]() - ² наименее значимая половина ²;
подобным же образом
- ² наименее значимая половина ²;
подобным же образом ![]() ,
, ![]() .
.
Например: Представим в подобной форме число ![]() .
.
Теперь мы
имеем ![]() .
.
Эта формула
сводит задачу умножения ![]() разрядных чисел к трем
операциям умножения
разрядных чисел к трем
операциям умножения ![]() разрядных чисел:
разрядных чисел: ![]() . Плюс некоторые прстые
операции сдвига и сложения. Эту формулу можно использовать для умножения с
двойной точностью, когда результат нужно получить с четверной точностью.При
помощи этой формулы можно определить некоторый рекурсивный процесс для
умножения, значительно более быстрый, чем уже знакомый нам метод, когда
. Плюс некоторые прстые
операции сдвига и сложения. Эту формулу можно использовать для умножения с
двойной точностью, когда результат нужно получить с четверной точностью.При
помощи этой формулы можно определить некоторый рекурсивный процесс для
умножения, значительно более быстрый, чем уже знакомый нам метод, когда ![]() - велико и имеющий время выполднения порядка
- велико и имеющий время выполднения порядка
![]() .
.
Если ![]() - время, необходимое для выполнения
умножения
- время, необходимое для выполнения
умножения ![]() - разрядных чисел, то мы имеем
- разрядных чисел, то мы имеем
![]() для некоторой константы
для некоторой константы ![]() , поскольку в правой части соотношения
требуется выполнить только три операции умножения плюс некоторые операции
сложения и сдвига. Из последнего соотношения по индукции вытекает, что
, поскольку в правой части соотношения
требуется выполнить только три операции умножения плюс некоторые операции
сложения и сдвига. Из последнего соотношения по индукции вытекает, что
![]() ,
,
если выбрать ![]() - достаточно большим, с тем , чтобы это
неравенство выполнялось при
- достаточно большим, с тем , чтобы это
неравенство выполнялось при ![]() , получим
, получим
![]()
То есть
время, затрачиваемое на умножение, можно сократить с величины порядка ![]() до величины порядка
до величины порядка ![]() , и, конечно, при большом
, и, конечно, при большом ![]()
этот алгоритм гораздо быстрее.
Похожий, но более сложный метод выполнения умножения с временем порядка
![]() был впервые предложен А.
Карацубой.
был впервые предложен А.
Карацубой.
Время выполнения можно сократить еще больше, если заметить,
что только что расмотренный метод является частным случаем (при ![]() ) более общего метода, который дает
) более общего метода, который дает
![]()
для любого фиксированного ![]() . Этот
более общий метод можно получить следующим образом. Разобьем
. Этот
более общий метод можно получить следующим образом. Разобьем
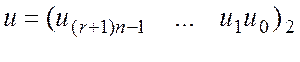 и
и 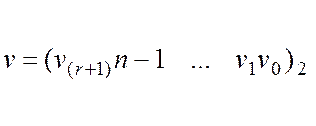
на ![]() частей:
частей:
![]()
![]()
где каждое ![]() и каждое
и каждое ![]() являются
являются ![]() разрядными
числами. Рассмотрим многочлены
разрядными
числами. Рассмотрим многочлены
![]() ,
, ![]()
и положим
![]() .
.
Так как ![]() и
и ![]() , то мы имеем
, то мы имеем ![]() , и
поэтому, если знать коэффициенты
, и
поэтому, если знать коэффициенты ![]() , можно легко вычислить
, можно легко вычислить
![]() . Задача состоит в том, чтобы найти хороший
способ вычисления коэффициентов
. Задача состоит в том, чтобы найти хороший
способ вычисления коэффициентов ![]() , выполняя лишь
, выполняя лишь ![]() операций умножения
операций умножения ![]() -
разрядных чисел плюс некоторые дополнительные операции, для которых время
выполнения пропорционально
-
разрядных чисел плюс некоторые дополнительные операции, для которых время
выполнения пропорционально ![]() .
.
Этого можно достичь вычисляя
![]() .
.
Коэффициенты всякого многочлена степени ![]() можно записать в виде линейной комбинации
значений этого многочлена в
можно записать в виде линейной комбинации
значений этого многочлена в ![]() различных точках.
Время, необходимое для взятия такой комбинации, самое большее пропорционально
различных точках.
Время, необходимое для взятия такой комбинации, самое большее пропорционально ![]() .В действительности произведения
.В действительности произведения ![]() являются, сторого говоря, не
произведениями
являются, сторого говоря, не
произведениями ![]() - разрядных чисел, а
произведениями чисел, разряд которых не превышает
- разрядных чисел, а
произведениями чисел, разряд которых не превышает ![]() , где
, где ![]() - фиксированная величина, зависящая от
- фиксированная величина, зависящая от ![]() . Легко составить программу умножения для
. Легко составить программу умножения для ![]() - разрядных чисел, которая требует
выполнения лишь
- разрядных чисел, которая требует
выполнения лишь ![]() операций, так как при
фиксированном
операций, так как при
фиксированном ![]() два произведения
два произведения ![]() - разрядных чисел на
- разрядных чисел на ![]() - разрядные можно получить за
- разрядные можно получить за ![]() операций.Можно показать, что для этого
метода
операций.Можно показать, что для этого
метода 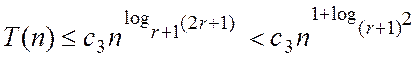 .
.
Теорема.
Для любого ![]() существует такая
постоянная
существует такая
постоянная ![]() и такой алгоритм умножения, что число
элементарных операций
и такой алгоритм умножения, что число
элементарных операций ![]() , которые необходимо выполнить,
чтобы умножить два
, которые необходимо выполнить,
чтобы умножить два ![]() -разрядных числа, удовлетворяет
оценке
-разрядных числа, удовлетворяет
оценке ![]() .
.
Эта теорема еще не самый лучший результат. Для практических
целей большой недостаток, что метод резко усложняется при ![]() т.е.
т.е. ![]() . Эта
теорема неудовлетворительна и с теоретической точки зрения, так как в ней не в
полной мере используется лежащий в ее основе метод многочленов.
. Эта
теорема неудовлетворительна и с теоретической точки зрения, так как в ней не в
полной мере используется лежащий в ее основе метод многочленов.
Прежде чем рассмотреть алгоритм Тоома-Кука, разберем один пример. На этом примере нельзя увидеть эффективность метода, поскольку мы имеем дело с небольшими числами. Но можно увидеть некоторые полезные упрощения, которые применимы в общем случае.
Пример.
Предположим, нам нужно умножить ![]() на
на ![]() . В двоичной системе счисления
. В двоичной системе счисления ![]() на
на ![]() . Пусть
. Пусть
![]() . Многочлены
. Многочлены ![]()
![]() ,
, ![]() .
.
Отсюда находим ![]() :
:
 (4.1)
(4.1)
Теперь, используя пять последних величин, найдем пять
коэффициентов многочлена ![]() .
.
Для нахождения коэффициентов многочлена
![]() при заданных значениях
при заданных значениях ![]() можно воспользоваться одним интересным
небольшим алгоритмом. Сначала запишем
можно воспользоваться одним интересным
небольшим алгоритмом. Сначала запишем
![]() , где
, где ![]()
![]() и где
и где ![]() неизвестны,
равно как и
неизвестны,
равно как и ![]() . Теперь
. Теперь
![]() , и по индукции находим, что для
всех
, и по индукции находим, что для
всех ![]()
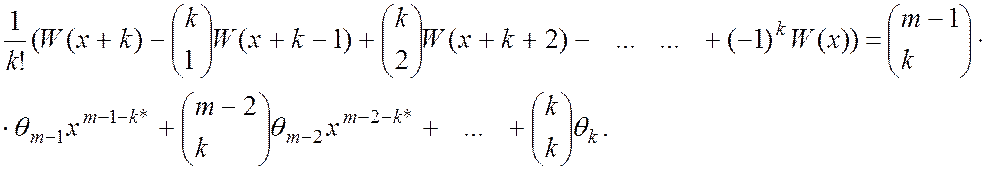
Обозначая левую часть выражения через 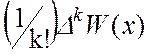 мы видим, что
мы видим, что
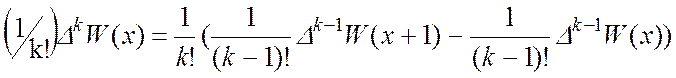
и 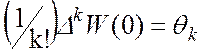 .
.
Таким образом, коэффициенты ![]() можно
вычислить с помощью очень простого метода, который можно продемонстрировать для
многочлена
можно
вычислить с помощью очень простого метода, который можно продемонстрировать для
многочлена ![]() , определенного соотношениями (4.1):
, определенного соотношениями (4.1):
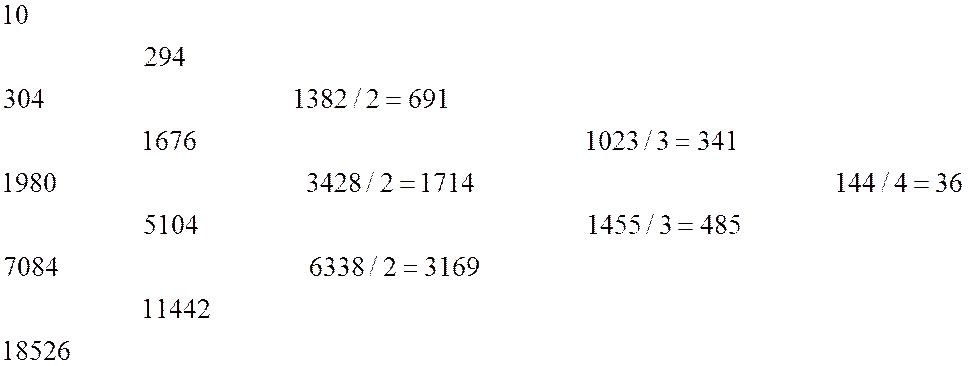
Крайняя колонка состоит из заданных значений ![]() ;чтобы
получить
;чтобы
получить ![]() -ю колонку, нужно вычислить разности между
соседними величинами предыдущей колонки и разделить их на
-ю колонку, нужно вычислить разности между
соседними величинами предыдущей колонки и разделить их на ![]() . Коеффициенты
. Коеффициенты ![]() располагаются
в колонках сверху; так,
располагаются
в колонках сверху; так, ![]() , поэтому мы имеем
, поэтому мы имеем
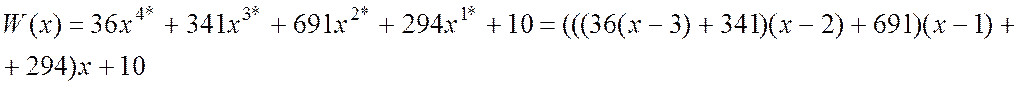 В общем виде можно записать
В общем виде можно записать
![]() эта формула показывает, каким
образом из коэфициентов
эта формула показывает, каким
образом из коэфициентов ![]() можно получить
коэффициенты
можно получить
коэффициенты ![]() :
:
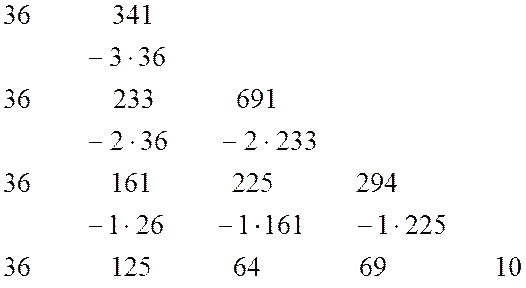
Последовательно получаются коэффициенты многочленов ![]() и т.д.
и т.д.
Согласно последней таблице мы имеем ![]()
Итак, ответом к нашей исходнй задаче будет ![]() где
где ![]() получается
в результате действий сложения и сдвига. Кроме того, если коэффициенты
многочлена
получается
в результате действий сложения и сдвига. Кроме того, если коэффициенты
многочлена ![]() - неотрицательны, то таковыми будут и
числа
- неотрицательны, то таковыми будут и
числа ![]() , а тогда все промежуточные результаты,
получаемые в процессе проведения вычисления, являются неотрицательными.
, а тогда все промежуточные результаты,
получаемые в процессе проведения вычисления, являются неотрицательными.
На этой идее основан алгоритм Тоома-Кука. Этот алгоритм позволяет существенно улучшить оценку сложности.
Теорема.
Существует константа ![]() , такая,
что время выполнения алгоритма С меньше
, такая,
что время выполнения алгоритма С меньше 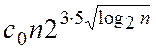 циклов.
циклов.
Задание. Найти методом Карацубы произведение
двух чисел ![]() и
и ![]() , где
, где ![]() - номер по журналу. Оценить сложность
вычислений.
- номер по журналу. Оценить сложность
вычислений.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.