Магнитомеханические явления. Электромагнитная индукция. Гармонические колебания. Затухающие колебания (Главы 4-7 учебного пособия по общей физике), страница 12

Частота w₁ – w₂, с которой изме-няется амплитуда результирующе-го колебания, называется частотой биений.

Величина 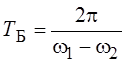 называ-ется периодом биений.

6.3.3. Сложение взаимно  перпендикулярных колебаний

Пусть материальная точка участвует одновременно в двух взаимно перпендикулярных колебаниях:

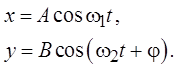
Точка, участвующая в таких колебаниях, будет одновременно двигаться вдоль двух осей – осей х и у. Поэтому траектория её движения в общем случае может не быть прямолинейной.

__________________________________

* Здесь использована тригонометрическая формула для суммы косинусов:
     cos x + cos y.

Найдём уравнение, описывающее траекторию частицы, участвующей в этих двух колебаниях, для наиболее простого случая (w₁ = w₂).

Для этого исключим из уравнений время t.

Из первого уравнения следует, что

;

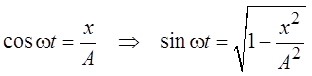а из второго уравнения вытекает

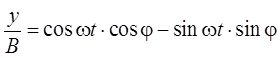
или

,

;

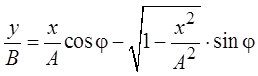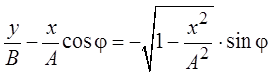возведем это выражение в квадрат

,

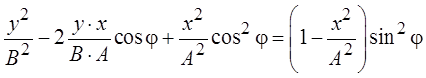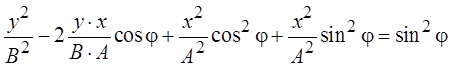
и, наконец, получим уравнение, описывающее траекторию движения частицы, участвующей в двух взаимно перпендику-лярных колебаниях:

.

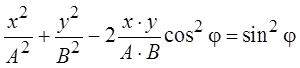Мы получили уравнение эллипса, длина и ориентация полуосей которого зависят от амплитуд складываемых коле-баний и от разности фаз j. Например, при равных амплитудах и разности фаз в 1 радиан эллипс имеет вид, показанный на рисунке.

Рассмотрим несколько частных слу-чаев.

1. Разность фаз j = 0.

В этом случае уравнение принимает вид

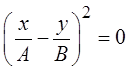
или

.

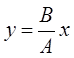Это уравнение прямой. Следователь-но, при такой разности фаз точка дви-жется по прямой линии. Её движение представляет собой гармоническое коле-бание с частотой w и амплитудой, равной .

Движение точки будет представлять со-бой гармоническое колебание и в том случае, когда j = p. Только прямая, вдоль которой будут происходить колебания, будет распо-ложена во втором и четвёртом квадрантах системы координат (проверьте это самосто-ятельно).

2. Разность фаз j = p/2.

В этом случае уравнение траектории принимает вид:

.

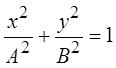Это уравнение эллипса, оси которого совпадают с осями координат.

Если амплитуды складываемых колебаний будут равны, точка будет двигаться по окружности.

Траектория будет такой же, как и в случае j =-p/2. Только точка будет двигаться в противоположную сторону.

Если частоты складываемых колебаний различны, форма траектории будет более сложной. Например, если частоты склады-ваемых колебаний отличаются в два раза, то траектория будет иметь вид, показанный на рисунке (если амплитуды складывае-мых колебаний равны и разность их фаз равна 1 радиан).

Кривые, описывающие траектории движения точки, участ-вующей в двух взаимно перпендику-лярных колебаниях, называют фигурами Лиссажу.

Фигуры Лиссажу позволяют опре-делить соотношение частот и разность фаз складываемых колебаний, что до сих пор используется на практике.

6.4.  Гармонический осциллятор

Осциллятор* – это любая система, которая может совершать колебания после того, как её вывели из положения равновесия. Если колебательная система совершает гармонические колебания, то она представляет собой гармо-нический осциллятор.

Поведение всех гармонических осцилляторов описывается дифференциальным уравнением *.

Это уравнение принято называть уравнением гармони-ческого осциллятора.

Решение такого дифференциального уравнения имеет вид . Аргумент х дифференциального уравнения совершает гармонические колебания.

Взяв первую и вторую производные по времени от х, получим, что и они совершают гармонические колебания , .

Гармонический осциллятор – это абстрактная модель, воспроизводящая реальные колебательные системы, в которых могут происходить гармонические колебания.

Рассмотрим некоторые из них.

________________________________

* Oscillo (лат.) – качаться.

6.4.1. Пружинный маятник

Пружинный маятник – это груз массой m, подвешенный на абсолютно упругой пружине, коэффициент упругости которой k.